练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】先化简，再求值： ，其中x=3tan30°+1．

    【答案】解： ÷（ ﹣ ）

    = ÷[ ﹣ ]

    = ÷

    =

    = ，

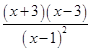
    当x=3tan30°+1=3× +1= +1时，

    原式= = =


    【解析】将原式除式的第一项分子分母同时乘以x+3，然后利用同分母分式的减法法则计算，将被除式分母利用平方差公式分解因式，除式分母利用平方差公式分解因式，分子利用完全平方公式分解因式，再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分得到最简结果，然后利用特殊角的三角函数值求出x的值，将x的值代入化简后的式子中计算，即可求出原式的值．
    【考点精析】根据题目的已知条件，利用特殊角的三角函数值的相关知识可以得到问题的答案，需要掌握分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，AB=2，将线段CD绕点C顺时针旋转90°得到线段CE，线段BD绕点B顺时针旋转90°得到线段BF，连接BF，则图中阴影部分的面积是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场销售一种夹克和衬衣，夹克每件定价100元，衬衣每件定价50元，商场在开展促销活动期间，向顾客提供两种优惠方案。

    方案一：买一件夹克送一件衬衣

    方案二：夹克和衬衣均按定价的80%付款

    现有顾客要到该商场购买夹克30件，衬衣x件（x>30）

    （1）若用方案一购买夹克需付款 元，衬衣需付款（用含x的式子表示） 元，共需付款 元。

    若用方案二购买夹克需付款 元，衬衣需付款（用含x的式子表示） 元，共需付款 元。

    （2）通过计算说明，购买衬衣多少件时，两种方案付款一样多？

    （3）当x=40时，哪种方案更省钱？请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个正整数能表示成两个连续偶数的平方差，那么这个正整数为“神秘数”.

    如：

    因此，4，12，20这三个数都是神秘数.

    （1）28和2012这两个数是不是神秘数？为什么？

    （2）设两个连续偶数为和(其中为非负整数)，由这两个连续偶数构造的神秘数是4的倍数，请说明理由.

    （3）两个连续奇数的平方差（取正数）是不是神秘数？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

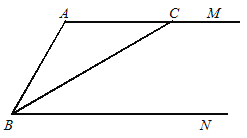
    【题目】如图，AM∥BN，BC是∠ABN的平分线.

    （1）过点A作AD⊥BC，垂足为O，AD与BN交于点D. （要求：用尺规作图，并在图中标明相应字母，保留作图痕迹，不写作法.）

    （2）求证：AC=BD.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O，与斜边AB交于点D、E为BC边的中点，连接DE．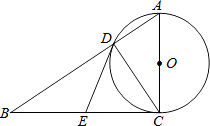
    （1）求证：DE是⊙O的切线；
    （2）填空：①若∠B=30°，AC=2 ，则DE=； ②当∠B=°时，以O，D，E，C为顶点的四边形是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

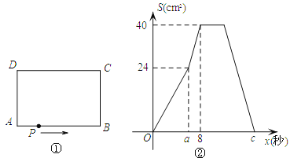
    【题目】如图①，在矩形ABCD中，AB=10cm，BC=8cm，点P从A出发，沿A→B→C→D路线运动，到D停止，点P的速度为每秒1cm，a秒时点P改变速度，变为每秒bcm，图②是点P出发x秒后△APD的面积S(cm2)与x(秒)的关系图象，

    (1)参照图②，求a、b及图②中的c值；

    (2)设点P离开点A的路程为y(cm)，请写出动点P改变速度后y与出发后的运动时间x(秒)的关系式，并求出点P到达DC中点时x的值．

    (3)当点P出发多少秒后，△APD的面积是矩形ABCD面积的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某个体户购进一批时令水果，20天销售完毕，他将本次销售情况进行了跟踪记录，根据所记录的数据绘制如下的函数图象，其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示，销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示。(销售额=销售单价×销售量)

    (1)直接写出y与x之间的函数解析式；

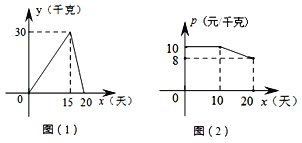
    (2)分别求第10天和第15天的销售额；

    (3)若日销售量不低于24千克的时间段为“最佳销售期”，则此次销售过程中，“最佳销售期”共有多少天?在此期间销售单价最高为多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

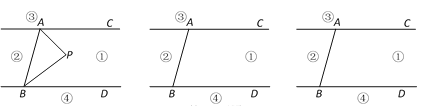
    【题目】如图，直线AC∥BD，连结AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连结PA、PB，构成∠PAC、∠APB、∠PBD三个角．(提示：有公共端点的两条重合的射线所组成的角是0°)

    (1)当动点P落在第①部分时，有∠APB＝∠PAC＋∠PBD，请说明理由；

    (2)当动点P落在第②部分时，∠APB＝∠PAC＋∠PBD是否成立？若不成立，试写出∠PAC、∠APB、∠PBD三个角的等量关系(无需说明理由)；

    (3)当动点P在第③部分时，探究∠PAC、∠APB、∠PBD之间的关系，写出你发现的一个结论并加以说明．

    查看答案和解析>>

    同步练习册答案