
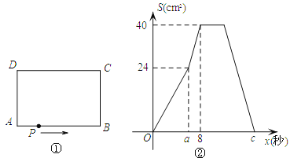
【题目】如图①,在矩形ABCD中,AB=10cm,BC=8cm,点P从A出发,沿A→B→C→D路线运动,到D停止,点P的速度为每秒1cm,a秒时点P改变速度,变为每秒bcm,图②是点P出发x秒后△APD的面积S(cm2)与x(秒)的关系图象,
(1)参照图②,求a、b及图②中的c值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的关系式,并求出点P到达DC中点时x的值.
(3)当点P出发多少秒后,△APD的面积是矩形ABCD面积的![]() .
.
【答案】(1)a=6,b = 2,c=17;(2)y=2x-6(6≤x≤17),x=![]() ;(3) 5秒和
;(3) 5秒和![]() 秒.
秒.
【解析】
(1)结合图象得出△APD随边长变化的规律,以及高的长度,可得出面积的变化情况,利用图表找出关键点当a秒时三角形面积是24,8秒时三角形面积是40,P到达B点,c秒时,P到达D点,即可求出;
(2)利用动点P改变速度后y与出发后的运动时间x的关系,直接写出关系式,根据P到达DC中点时,y=10+8+10×![]() =23,代入关系式,即可求出点P到达DC中点时x的值;(3)根据题意可知当P在AB中点和CD中点时,△APD的面积是矩形ABCD面积的
=23,代入关系式,即可求出点P到达DC中点时x的值;(3)根据题意可知当P在AB中点和CD中点时,△APD的面积是矩形ABCD面积的![]() ,分别由P在这两点时运动的路程即可求出.
,分别由P在这两点时运动的路程即可求出.
(1)由图得知:S△APD=![]() AD·AP=
AD·AP=![]() ×8×1×a=24
×8×1×a=24
∴a=6 b=![]() = 2 c=8+
= 2 c=8+![]() =17
=17
(2)y=6+2(x-6)=2x-6(6≤x≤17)
P到达DC中点时,y=10+8+10×![]() =23
=23
即23=2x-6 x=![]()
(3)当P在AB中点和CD中点时,S△APD=![]() S矩形ABCD
S矩形ABCD
当P在AB中点时,P出发5秒;
当P在CD中点时,代入(2)中y=2x-6
即23=2x-6 x=![]()
∴P出发5秒和![]() 秒时,S△APD=
秒时,S△APD=![]() S矩形ABCD..
S矩形ABCD..


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
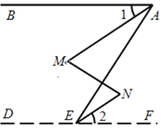
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE(______).
∴∠BAE=∠AEF(______).
又∵∠1=∠2(已知)
∴ ∠BAE∠1=∠AEF_____(等式性质),即 ∠MAE = ∠NEA .
∴_______∥______(______).
∴∠M=∠N(两直线平行,内错角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)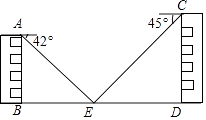
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解题过程.
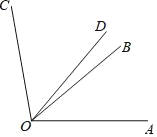
已知:如图,∠AOB=40°,∠BOC=60°,OD平分∠AOC.求∠BOD的度数.
解:∵∠AOC=∠AOB+∠ ,
又∵∠AOB=40°,∠BOC=60°,
∴∠AOC= °.
∵OD平分∠AOC,
∴∠AOD= ∠AOC( ).
∴∠AOD=50°.
∴∠BOD=∠AOD﹣∠ .
∴∠BOD= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com