
ЁОЬтФПЁПФГИіЬхЛЇЙКНјвЛХњЪБСюЫЎЙћЃЌ20ЬьЯњЪлЭъБЯЃЌЫћНЋБОДЮЯњЪлЧщПіНјааСЫИњзйМЧТМЃЌИљОнЫљМЧТМЕФЪ§ОнЛцжЦШчЯТЕФКЏЪ§ЭМЯѓЃЌЦфжаШеЯњЪлСПy(ЧЇПЫ)гыЯњЪлЪБМфx(Ьь)жЎМфЕФКЏЪ§ЙиЯЕШчЭМ(1)ЫљЪОЃЌЯњЪлЕЅМлp(дЊ/ЧЇПЫ)гыЯњЪлЪБМфx(Ьь)жЎМфЕФКЏЪ§ЙиЯЕШчЭМ(2)ЫљЪОЁЃ(ЯњЪлЖю=ЯњЪлЕЅМлЁСЯњЪлСП)
(1)жБНгаДГіyгыxжЎМфЕФКЏЪ§НтЮіЪНЃЛ
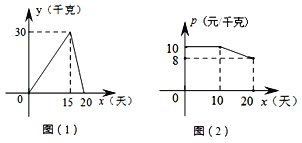
(2)ЗжБ№ЧѓЕк10ЬьКЭЕк15ЬьЕФЯњЪлЖюЃЛ
(3)ШєШеЯњЪлСПВЛЕЭгк24ЧЇПЫЕФЪБМфЖЮЮЊЁАзюМбЯњЪлЦкЁБЃЌдђДЫДЮЯњЪлЙ§ГЬжаЃЌЁАзюМбЯњЪлЦкЁБЙВгаЖрЩйЬь?дкДЫЦкМфЯњЪлЕЅМлзюИпЮЊЖрЩйдЊ?
ЁОД№АИЁПНтЃКЃЈ1ЃЉ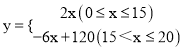 ЁЃ
ЁЃ
ЃЈ2ЃЉЁпЕк10ЬьКЭЕк15ЬьдкЕк10ЬьКЭЕк20ЬьжЎМфЃЌ
ЁрЕБ10ЁмxЁм20ЪБЃЌЩшЯњЪлЕЅМлpЃЈдЊ/ЧЇПЫЃЉгыЯњЪлЪБМфxЃЈЬьЃЉжЎМфЕФКЏЪ§НтЮіЪНЮЊp=mx+nЃЌ
ЁпЕуЃЈ10ЃЌ10ЃЉЃЌЃЈ20ЃЌ8ЃЉдкz=mx+nЕФЭМЯѓЩЯЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК 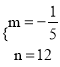 ЁЃ
ЁЃ
Ёр![]() ЁЃ
ЁЃ
ЕБx=10ЪБЃЌ ![]() ЃЌy=2ЁС10=20ЃЌЯњЪлН№ЖюЮЊЃК10ЁС20=200ЃЈдЊЃЉЃЛ
ЃЌy=2ЁС10=20ЃЌЯњЪлН№ЖюЮЊЃК10ЁС20=200ЃЈдЊЃЉЃЛ
ЕБx=15ЪБЃЌ ![]() ЃЌy=2ЁС15=30ЃЌЯњЪлН№ЖюЮЊЃК9ЁС30=270ЃЈдЊЃЉЁЃ
ЃЌy=2ЁС15=30ЃЌЯњЪлН№ЖюЮЊЃК9ЁС30=270ЃЈдЊЃЉЁЃ
ЙЪЕк10ЬьКЭЕк15ЬьЕФЯњЪлН№ЖюЗжБ№ЮЊ200дЊЃЌ270дЊЁЃ
ЃЈ3ЃЉШєШеЯњЪлСПВЛЕЭгк24ЧЇПЫЃЌдђyЁн24ЁЃ
ЕБ0ЁмxЁм15ЪБЃЌy=2xЃЌ
НтВЛЕШЪН2xЁн24ЃЌЕУxЁн12ЃЛ
ЕБ15ЃМxЁм20ЪБЃЌy=Љ6x+120ЃЌ
НтВЛЕШЪНЉ6x+120Ён24ЃЌЕУxЁм16ЁЃ
Ёр12ЁмxЁм16ЁЃ
ЁрЁАзюМбЯњЪлЦкЁБЙВгаЃК16Љ12+1=5ЃЈЬьЃЉЁЃ
Ёп![]() ЃЈ10ЁмxЁм20ЃЉжа
ЃЈ10ЁмxЁм20ЃЉжа![]() ЃМ0ЃЌЁрpЫцxЕФдіДѓЖјМѕаЁЁЃ
ЃМ0ЃЌЁрpЫцxЕФдіДѓЖјМѕаЁЁЃ
ЁрЕБ12ЁмxЁм16ЪБЃЌxШЁ12ЪБЃЌpгазюДѓжЕЃЌДЫЪБ![]() =9.6ЃЈдЊ/ЧЇПЫЃЉЁЃ
=9.6ЃЈдЊ/ЧЇПЫЃЉЁЃ
ЙЪДЫДЮЯњЪлЙ§ГЬжаЁАзюМбЯњЪлЦкЁБЙВга5ЬьЃЌдкДЫЦкМфЯњЪлЕЅМлзюИпЮЊ9.6дЊ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЗжСНжжЧщПіНјааЬжТлЃКЂй0ЁмxЁм15ЃЛЂк15ЃМxЁм20ЃЌеыЖдУПвЛжжЧщПіЃЌЖМПЩвдЯШЩшГіКЏЪ§ЕФНтЮіЪНЃЌдйНЋвбжЊЕуЕФзјБъДњШыЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтЃК
ЂйЕБ0ЁмxЁм15ЪБЃЌЩшШеЯњЪлСПyгыЯњЪлЪБМфxЕФКЏЪ§НтЮіЪНЮЊy=k1xЃЌ
ЁпжБЯпy=k1xЙ§ЕуЃЈ15ЃЌ30ЃЉЃЌЁр15k1=30ЃЌНтЕУk1=2ЁЃ
Ёрy=2xЃЈ0ЁмxЁм15ЃЉЃЛ
ЂкЕБ15ЃМxЁм20ЪБЃЌЩшШеЯњЪлСПyгыЯњЪлЪБМфxЕФКЏЪ§НтЮіЪНЮЊy=k2x+bЃЌ
ЁпЕуЃЈ15ЃЌ30ЃЉЃЌЃЈ20ЃЌ0ЃЉдкy=k2x+bЕФЭМЯѓЩЯЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЁЃ
ЁЃ
Ёрy=Љ6x+120ЃЈ15ЃМxЁм20ЃЉЁЃ
злЩЯЫљЪіЃЌПЩжЊyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃК 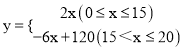 ЁЃ
ЁЃ
ЃЈ2ЃЉШеЯњЪлН№Жю=ШеЯњЪлЕЅМлЁСШеЯњЪлСПЃЎгЩгкЕк10ЬьКЭЕк15ЬьдкЕк10ЬьКЭЕк20ЬьжЎМфЃЌЕБ10ЁмxЁм20ЪБЃЌЩшЯњЪлЕЅМлpЃЈдЊ/ЧЇПЫЃЉгыЯњЪлЪБМфxЃЈЬьЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊp=mx+nЃЌгЩЕуЃЈ10ЃЌ10ЃЉЃЌЃЈ20ЃЌ8ЃЉдкp=mx+nЕФЭМЯѓЩЯЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЕУpгыxЕФКЏЪ§НтЮіЪНЃЌМЬЖјЧѓЕУ10ЬьгыЕк15ЬьЕФЯњЪлН№ЖюЁЃ
ЃЈ3ЃЉШеЯњЪлСПВЛЕЭгк24ЧЇПЫЃЌМДyЁн24ЃЎЯШНтВЛЕШЪН2xЁн24ЃЌЕУxЁн12ЃЌдйНтВЛЕШЪНЉ6x+120Ён24ЃЌЕУxЁм16ЃЌдђЧѓГіЁАзюМбЯњЪлЦкЁБЙВга5ЬьЃЛШЛКѓИљОн![]() ЃЈ10ЁмxЁм20ЃЉЃЌРћгУвЛДЮКЏЪ§ЕФаджЪЃЌМДПЩЧѓГідкДЫЦкМфЯњЪлЪБЕЅМлЕФзюИпжЕЁЃ
ЃЈ10ЁмxЁм20ЃЉЃЌРћгУвЛДЮКЏЪ§ЕФаджЪЃЌМДПЩЧѓГідкДЫЦкМфЯњЪлЪБЕЅМлЕФзюИпжЕЁЃ


 УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ![]() гы
гы![]() ЖМЪЧвд
ЖМЪЧвд![]() ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌ ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ ![]() ЃЌЕБ
ЃЌЕБ![]() ЪЧжБНЧШ§НЧаЮЪБЃЌдђ
ЪЧжБНЧШ§НЧаЮЪБЃЌдђ![]() ЕФГЄЮЊ__________ЃЎ
ЕФГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
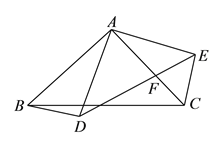
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌжаЯпBEЃЌCDНЛгкЕуOЃЌFЃЌGЗжБ№ЪЧOBЃЌOCЕФжаЕуЃЌСЌНгDFЃЌFGЃЌEGЃЌDEЃЌЧѓжЄЃКDFЃНEG.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
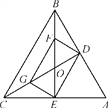
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЌЕуPЮЊЁїABCЫљдкЦНУцФквЛЕуЃЌЙ§ЕуPЗжБ№зїPEЁЮACНЛABгкЕуEЃЌPFЁЮABНЛBCгкЕуDЃЌНЛACгкЕуFЃЎ
ЁО1ЁПШчЭМ1ЃЌШєЕуPдкBCБпЩЯЃЌДЫЪБPD=0ЃЌвзжЄPDЃЌPEЃЌPFгыABТњзуЕФЪ§СПЙиЯЕPD+PE+PF=ABЃЛЕБЕуPдкЁїABCФкЃЌЯШдкЭМ2жазїГіЭМаЮЃЌВЂаДГіPDЃЌPEЃЌPFгыABТњзуЕФЪ§СПЙиЯЕЃЌШЛКѓжЄУїФуЕФНсТл
ЁО2ЁПЕБЕуPдкЁїABCЭтЃЌЯШдкЭМ3жазїГіЭМаЮЃЌШЛКѓаДГіPDЃЌPEЃЌPFгыABТњзуЕФЪ§СПЙиЯЕЃЎЃЈВЛгУЫЕУїРэгЩЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаБфаЮе§ШЗЕФЪЧ( )
A. 4xЉ5ЃН3x+2БфаЮЕУ 4xЉ3xЃН2Љ5
B. ![]() БфаЮЕУxЃН1
БфаЮЕУxЃН1
C. 3(xЉ1)ЃН2(x+3)БфаЮЕУ3xЉ1ЃН2x+6
D. ![]() БфаЮЕУ3xЃН15
БфаЮЕУ3xЃН15
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇаЁзщЕФСНЮЛЭЌбЇзМБИВтСПСНДБНЬбЇТЅжЎМфЕФОрРыЃЌШчЭМЃЌСНДБНЬбЇТЅABКЭCDжЎМфгавЛОАЙлГиЃЈABЁЭBDЃЌCDЁЭBDЃЉЃЌвЛЭЌбЇдкAЕуВтЕУГижаХчШЊДІEЕуЕФИЉНЧЮЊ42ЁуЃЌСэвЛЭЌбЇдкCЕуВтЕУEЕуЕФИЉНЧЮЊ45ЁуЃЈЕуBЃЌEЃЌDдкЭЌвЛжБЯпЩЯЃЉЃЌСНИіЭЌбЇвбОдкбЇаЃзЪСЯЪвВщГіТЅИпAB=15mЃЌCD=20mЃЌЧѓСНДБНЬбЇТЅжЎМфЕФОрРыBDЃЎ
ЃЈНсЙћОЋШЗЕН0.1mЃЌВЮПМЪ§ОнЃКsin42ЁуЁж0.67ЃЌcos42ЁуЁж0.74ЃЌtan42ЁуЁж0.90ЃЉ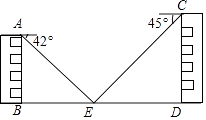
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаЕШЪНЃКЃЈ1ЃЉ13ЃН![]() ЁС12ЁС22ЃЛЃЈ2ЃЉ13+23ЃН
ЁС12ЁС22ЃЛЃЈ2ЃЉ13+23ЃН![]() ЁС22ЁС32ЃЛЃЈ3ЃЉ13+23+33ЃН
ЁС22ЁС32ЃЛЃЈ3ЃЉ13+23+33ЃН![]() ЁС32ЁС42ЃЛЃЈ4ЃЉ13+23+33+43ЃН
ЁС32ЁС42ЃЛЃЈ4ЃЉ13+23+33+43ЃН![]() ЁС42ЁС52ЃЛ
ЁС42ЁС52ЃЛ![]()
ИљОнЩЯЪіЕШЪНЕФЙцТЩЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіЕк5ИіЕШЪНЃК_____ЃЛ
ЃЈ2ЃЉаДГіЕкnИіЕШЪНЃЈгУКЌгаnЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉЩшsЪЧе§ећЪ§ЧвsЁн2ЃЌгІгУФуЗЂЯжЕФЙцТЩЃЌЛЏМђЃК![]() ЁСs2ЁСЃЈs+1ЃЉ2Љ
ЁСs2ЁСЃЈs+1ЃЉ2Љ![]() ЁСЃЈsЉ1ЃЉ2ЁСs2ЃЎ
ЁСЃЈsЉ1ЃЉ2ЁСs2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫГЗсПьЕнЙЋЫОХЩМзЁЂввСНГЕДгAЕиНЋвЛХњЮяЦЗдШЫйдЫЭљBЕиЃЌМзГіЗЂ0.5hКѓввПЊЪМГіЗЂЃЌНсЙћБШМздч1ЃЈhЃЉЕНДяBЕиЃЌШчЭМЃЌЯпЖЮOPЁЂMNЗжБ№БэЪОМзЁЂввСНГЕРыAЕиЕФОрРыSЃЈkmЃЉгыЪБМфtЃЈhЃЉЕФЙиЯЕЃЌaБэЪОAЁЂBСНЕижЎМфЕФОрРыЃЎЧыНсКЯЭМжаЕФаХЯЂНтОіШчЯТЮЪЬтЃК 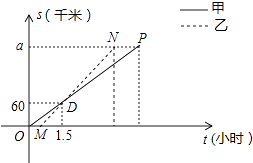
ЃЈ1ЃЉЗжБ№МЦЫуМзЁЂввСНГЕЕФЫйЖШМАaЕФжЕЃЛ
ЃЈ2ЃЉввГЕЕНДяBЕиКѓвддЫйСЂМДЗЕЛиЃЌЧыЮЪМзГЕЕНДяBЕиКѓвдЖрДѓЕФЫйЖШСЂМДдШЫйЗЕЛиЃЌВХФмгыввГЕЭЌЪБЛиЕНAЕиЃПВЂдкЭМжаЛГіМзЁЂввСНГЕдкЗЕЛиЙ§ГЬжаРыAЕиЕФОрРыSЃЈkmЃЉгыЪБМфtЃЈhЃЉЕФКЏЪ§ЭМЯѓЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com