
【题目】下列变形正确的是( )
A. 4x﹣5=3x+2变形得 4x﹣3x=2﹣5
B. ![]() 变形得x=1
变形得x=1
C. 3(x﹣1)=2(x+3)变形得3x﹣1=2x+6
D. ![]() 变形得3x=15
变形得3x=15
【答案】D
【解析】
利用去括号,移项,合并同类项,不等式的性质对四个选项逐一分析,即可得出答案.
解:选项A,4x﹣5=3x+2变形得 4x﹣3x=2+5,
﹣5从左边移项到右边要变号,而选项A没变号,
∴选项A错误,故选项A不符合题意;
选项B,方程两边同时乘以![]() ,而选项B方程左边乘以
,而选项B方程左边乘以![]() ,右边乘以
,右边乘以![]() ,
,
不满足不等式的性质2,
∴选项B错误,故选项B不符合题意;
选项C,去括号得,3(x﹣1)=2(x+3)变形得,3x﹣3=2x+6,
而去括号时,左边的﹣1没乘以3,
∴选项C错误,故选项C不符合题意;
选项D,去分母得,5(x﹣1)﹣2x=10,去括号得,5x﹣5﹣2x=10,
移项得,5x﹣2x=10+5,合并同类项得,3x=15,
∴选项D正确,符合题意.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE. 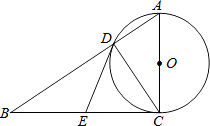
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2 ![]() ,则DE=; ②当∠B=°时,以O,D,E,C为顶点的四边形是正方形.
,则DE=; ②当∠B=°时,以O,D,E,C为顶点的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体户购进一批时令水果,20天销售完毕,他将本次销售情况进行了跟踪记录,根据所记录的数据绘制如下的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示。(销售额=销售单价×销售量)
(1)直接写出y与x之间的函数解析式;
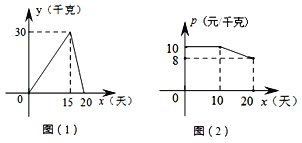
(2)分别求第10天和第15天的销售额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中,“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题,“计算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]() ﹣
﹣![]() )÷(﹣
)÷(﹣![]() )…第一步
)…第一步
=(![]() ﹣
﹣![]() )×(﹣12)…第二步
)×(﹣12)…第二步
=﹣4+10…第三步
=6…第四步
所以(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )=
)=![]() .
.
(1)小明解法第二步到第三步的运算依据是什么?
(2)请你运用小明的解法计算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() +
+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B分别为数轴上的两点,点A表示的数是﹣30,点B表示的数是50.
(1)请直接写出线段AB中点M表示的数_____;
(2)现有一直蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一只蚂蚁Q恰好从点A出发,以每秒2个单位长度的速度沿数轴向右移动,设两只蚂蚁在数轴上的点C相遇,求点C对应的数是多少?
(3)若蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左运动,同时另一只蚂蚁Q恰好从A点出发,以每秒2个单位长度的速度沿数轴也向左运动.设Q蚂蚁在数轴上D点时,P蚂蚁与它相距10个单位,求D点表示的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,且AC=DF,连接AC、DF.求证:∠A=∠D.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A﹣B﹣C﹣O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )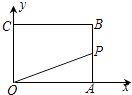
A.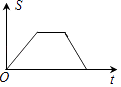
B.
C.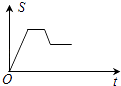
D.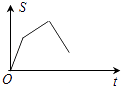
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com