
����Ŀ����ѧ��ʦ������һ��˼���⣬�����㣺(��![]() )��(
)��(![]() ��
��![]() )����С����ϸ˼����һ��������һ�ֲ�ͬ�ķ��������������⣮
)����С����ϸ˼����һ��������һ�ֲ�ͬ�ķ��������������⣮
С���Ľⷨ��ԭʽ�ĵ���Ϊ(![]() ��
��![]() )��(��
)��(��![]() )����һ��
)����һ��
��(![]() ��
��![]() )��(��12)���ڶ���
)��(��12)���ڶ���
����4+10��������
��6�����IJ�
����(��![]() )��(
)��(![]() ��
��![]() )��
)��![]() ��
��
(1)С���ⷨ�ڶ�����������������������ʲô��
(2)��������С���Ľⷨ���㣺(��![]() )��(
)��(![]() ��
��![]() +
+![]() )��
)��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���¹���Ʒ�֣�ij���ƻ��¹���A��B����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����A����ĵ���Ϊ7Ԫ/�ã�����B�����������y��Ԫ���빺������x���ã�֮�������ͼ��ʾ�ĺ�����ϵ�� 
��1����y��x�ĺ�����ϵʽ��
��2�����ڹ���ƻ��У�B���������������35�ã���������A���������������ƹ�����ʹ�ܷ�����ͣ��������ͷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
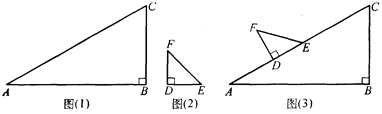
����Ŀ��ijͬѧ��һ�ο����У���ӲֽƬ��������ֱ�������Σ���ͼ(1)��ͼ(2)����ͼ(1)�У���B=90������A=30����ͼ(2)�У���D=90������F=45����ͼ(3)�Ǹ�ͬѧ������һ��ʵ�飺������DEF��ֱ�DZ�DE����ABC��б��AC�غ���һ�𣬲�����DEF��AC�����ƶ������ƶ������У�D��E����ʼ����AC���ϣ��ƶ���ʼʱ����D���A�غϣ�
(1)��DEF���ƶ������У���FCE���CFE����֮���Ƿ�Ϊ��ֵ�������˵����
(2)�ܷ���DEF�ƶ���ijλ�ã�ʹF��C��������ABƽ��?���ܣ������CFE�Ķ����������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��ͼ���һ֧λ�ڵ�һ���ޣ�
��ͼ���һ֧λ�ڵ�һ���ޣ�
��1���жϸú���ͼ�����һ֧���ڵ����ޣ�����m��ȡֵ��Χ��
��2����ͼ��OΪ����ԭ�㣬��A�ڸ÷���������λ�ڵ�һ����ͼ���ϣ���B���A����![]() ��Գƣ�����OAB�����Ϊ6����m��ֵ��
��Գƣ�����OAB�����Ϊ6����m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����б�����ȷ����( )
A. 4x��5��3x+2���ε� 4x��3x��2��5
B. ![]() ���ε�x��1
���ε�x��1
C. 3(x��1)��2(x+3)���ε�3x��1��2x+6
D. ![]() ���ε�3x��15
���ε�3x��15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ�ĸ����У�������
����ֱ֪�������ε����Ϊ2����ֱ�DZߵı�Ϊ1��2����б�߳�Ϊ![]() ��
��
��ֱ�������ε����߳�Ϊ![]() ����̱߳�Ϊ1������һ�߳�Ϊ
����̱߳�Ϊ1������һ�߳�Ϊ![]() ��
��
���ڡ�ABC�У�����A����B����C=1��5��6�����ABCΪֱ�������Σ�
�ܵ������������Ϊ12���ױ��ϵĸ�Ϊ4��������Ϊ5��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ� �Ͽ�ʱ����ʦ�������һ�����⣺��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ��
С�ݵ�˼·�ǣ�ԭ����ʽ�ȼ���x2��2x��1��a���躯��y1=x2��2x��1��y2=a����������������ͼ���ʾ��ͼ������ԭ����ת��Ϊ����y1��ͼ����y2��ͼ���Ϸ�ʱa��ȡֵ��Χ��
����С�ݵ�˼·�ش�
��������ʵ��x������x�IJ���ʽx2��2x��1��a��0���������a��ȡֵ��Χ�ǣ�
�ο�С��˼������ķ�����������⣺
����x�ķ���x��4= ![]() ��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
��0��a��4��Χ���������⣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�У�AD����BAC�Ľ�ƽ���ߣ�EΪAD��һ�㣬��BEΪһ������BE�·����ȱ���BEF������CF.

(1)��֤��AE��CF��
(2)����ACF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABCΪ���������Σ�AB��AC����DΪֱ��BC��һ���㣨��D�����B����C�غϣ�����ADΪ������ADE����AD��AE������CE����BAC����DAE��
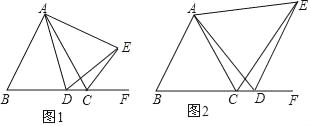
��1����ͼ1������D�ڱ�BC��ʱ����˵�����١�ABD�ա�ACE����BC��DC+CE��
��2����ͼ2������D�ڱ�BC���ӳ�����ʱ�������������䣬̽���߶�BC��DC��CE֮����ڵ�������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com