
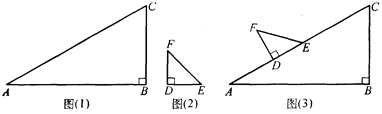
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图(1)、图(2).在图(1)中,∠B=90°,∠A=30°;图(2)中,∠D=90°,∠F=45°.图(3)是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上,移动开始时,点D与点A重合.
(1)△DEF在移动过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
科目:初中数学 来源: 题型:
【题目】请观察下列算式,找出规律并填空
①![]() =1﹣
=1﹣![]() ,②
,②![]() =
=![]() ×(1﹣
×(1﹣![]() ),③
),③![]() =
=![]() ×(1﹣
×(1﹣![]() ),④
),④![]() =
=![]() ×(1﹣
×(1﹣![]() ),…
),…
(1)则第10个算式是______,
(2)第n个算式为_______=_______.
(3)从以上规律中你可得到一些启示吗?根据你得到的启示,试解答下题:
若有理数a、b满足|a﹣1|+(b﹣3)2=0,
求![]() +
+![]() +
+![]() +…+
+…+![]() 的值.
的值.
(4)如图,把一个面积为1的正方形等分成两个面积为![]() 的长方形,接着把面积为
的长方形,接着把面积为![]() 的长方形等分成两个面积为
的长方形等分成两个面积为![]() 的正方形,再把面积为
的正方形,再把面积为![]() 的正方形等分成两个面积为
的正方形等分成两个面积为![]() 的矩形.如此进行下去,试利用图形揭示的规律计算:
的矩形.如此进行下去,试利用图形揭示的规律计算:![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() (直接写答案)
(直接写答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm、s的速度移动.如果P、Q同时出发,用![]() (秒)表示移动的时间,那么:
(秒)表示移动的时间,那么:
(1)如图1,当![]() 为何值时,△QAP为等腰直角三角形?
为何值时,△QAP为等腰直角三角形?
(2)如图2,当![]() 为何值时,△QAB的面积等于长方形面积的
为何值时,△QAB的面积等于长方形面积的![]()
(3)如图3,P、Q到达B、A后继续运动,P点到达C点后都停止运动.当![]() 为何值时,线段AQ的长等于线段CP的长的一半?
为何值时,线段AQ的长等于线段CP的长的一半?
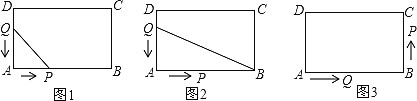
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE. 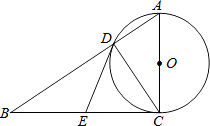
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2 ![]() ,则DE=; ②当∠B=°时,以O,D,E,C为顶点的四边形是正方形.
,则DE=; ②当∠B=°时,以O,D,E,C为顶点的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两正数a、b之间的一种运算,记作:(a,b),如果![]() ,那么(a,b)=c例如
,那么(a,b)=c例如![]() ,所以(2,8)=3
,所以(2,8)=3
(1)填空:(3,27)=_____,![]() =_____;
=_____;
(2)小明在研究这种运算时发现一个现象:![]() 小明给出了如下的证明:
小明给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]() .
.
所以![]() ,即(3,4)=x,所以(3n,4n)
,即(3,4)=x,所以(3n,4n)![]() 请你尝试运用这种方法说明下面这个等式成立:
请你尝试运用这种方法说明下面这个等式成立:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题,“计算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]() ﹣
﹣![]() )÷(﹣
)÷(﹣![]() )…第一步
)…第一步
=(![]() ﹣
﹣![]() )×(﹣12)…第二步
)×(﹣12)…第二步
=﹣4+10…第三步
=6…第四步
所以(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )=
)=![]() .
.
(1)小明解法第二步到第三步的运算依据是什么?
(2)请你运用小明的解法计算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() +
+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 任意抛掷一个啤酒瓶盖,落地后印有商标一面向上的可能性大小是![]()
B. 一个转盘被分成8块全等的扇形区域,其中2块是红色,6块是蓝色. 用力转动转盘,当转盘停止后,指针对准红色区域的可能性大小是![]()
C. 一个不透明的盒子中装有2个白球,3个红球,这些球除颜色外都相同. 从这个盒子中随意摸出一个球,摸到白球的可能性大小是![]()
D. 100件同种产品中,有3件次品. 质检员从中随机取出一件进行检测,他取出次品的可能性大小是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com