
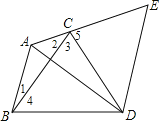
【题目】已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.

【答案】(1)60°;(2)5.
【解析】
试题分析:根据等边三角形的性质由△BCD为等边三角形得到∠3=∠4=60°,DC=DB,再根据旋转的性质得到∠5=∠1+∠4=∠1+60°,则∠2+∠3+∠5=∠2+∠1+120°,再根据三角形内角和定理得到
∠1+∠2=180°-∠BAC=60°,于是∠2+∠3+∠5=60°+120°=180°,即可得到点A、C、E在一条直线上;
由于点A、C、E在一条直线上,△ABD绕着点D按顺时针方向旋转60°后得到△ECD,则∠ADE=60°,DA=DE,得到△ADE为等边三角形,则∠DAE=60°,然后利用∠BAD=∠BAC-∠DAE计算即可;
由于点A、C、E在一条直线上,则AE=AC+CE,根据旋转的性质得到CE=AB,则AE=AC+AB=2+3=5,而△ADE为等边三角形,则AD=AE=5.
试题解析:∵△BCD为等边三角形,∴∠3=∠4=60°,DC=DB,∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD,∴∠5=∠1+∠4=∠1+60°,∴∠2+∠3+∠5=∠2+∠1+120°,∵∠BAC=120°,
∴∠1+∠2=180°-∠BAC=60°,∴∠2+∠3+∠5=60°+120°=180°,∴点A、C、E在一条直线上;∵点A、C、E在一条直线上,而△ABD绕着点D按顺时针方向旋转60°后得到△ECD,∴∠ADE=60°,DA=DE,
∴△ADE为等边三角形,∴∠DAE=60°,∴∠BAD=∠BAC-∠DAE=120°-60°=60°;
∵点A、C、E在一条直线上,∴AE=AC+CE,∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD,
∴CE=AB,∴AE=AC+AB=2+3=5,∵△ADE为等边三角形,∴AD=AE=5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为 ![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系. 
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣ ![]() x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.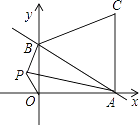
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a, ![]() ),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值.
),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3,﹣1, ![]() ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组  无解,且使关于x的分式方程
无解,且使关于x的分式方程 ![]() =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣2
B.﹣3
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
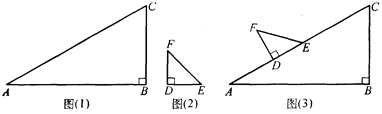
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图(1)、图(2).在图(1)中,∠B=90°,∠A=30°;图(2)中,∠D=90°,∠F=45°.图(3)是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上,移动开始时,点D与点A重合.
(1)△DEF在移动过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 上课时李老师提出这样一个问题:对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,求a的取值范围.
小捷的思路是:原不等式等价于x2﹣2x﹣1>a,设函数y1=x2﹣2x﹣1,y2=a,画出两个函数的图象的示意图,于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围.
请结合小捷的思路回答:
对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,则a的取值范围是.
参考小捷思考问题的方法,解决问题:
关于x的方程x﹣4= ![]() 在0<a<4范围内有两个解,求a的取值范围.
在0<a<4范围内有两个解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com