
【题目】请观察下列算式,找出规律并填空
①![]() =1﹣
=1﹣![]() ,②
,②![]() =
=![]() ×(1﹣
×(1﹣![]() ),③
),③![]() =
=![]() ×(1﹣
×(1﹣![]() ),④
),④![]() =
=![]() ×(1﹣
×(1﹣![]() ),…
),…
(1)则第10个算式是______,
(2)第n个算式为_______=_______.
(3)从以上规律中你可得到一些启示吗?根据你得到的启示,试解答下题:
若有理数a、b满足|a﹣1|+(b﹣3)2=0,
求![]() +
+![]() +
+![]() +…+
+…+![]() 的值.
的值.
(4)如图,把一个面积为1的正方形等分成两个面积为![]() 的长方形,接着把面积为
的长方形,接着把面积为![]() 的长方形等分成两个面积为
的长方形等分成两个面积为![]() 的正方形,再把面积为
的正方形,再把面积为![]() 的正方形等分成两个面积为
的正方形等分成两个面积为![]() 的矩形.如此进行下去,试利用图形揭示的规律计算:
的矩形.如此进行下去,试利用图形揭示的规律计算:![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() (直接写答案)
(直接写答案)

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】南宋数学家杨辉在研究(a+b)n展开式各项的系数时,采用了特殊到一般的方法,他将(a+b)0,(a+b)1,(a+b)2,(a+b)3,…,展开后各项的系数画成如图所示的三角阵,在数学上称之为杨辉三角.已知(a+b)0=1,(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3.按杨辉三角写出(a+b)5的展开式是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为 ![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,点A(0,0)、B(4 ![]() ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …则第2017个等边三角形的边长等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴打车为市民的出行带来了很大的方便,小亮调查了若干市民一周内使用滴滴打车的时间t(单位:分),将获得的数据分成四组,绘制了如下统计图,请根据图中信息,解答下列问题: 
(1)这次被调查的总人数是多少?
(2)试求表示C组的扇形圆心角的度数,并补全条形统计图;
(3)若全市的总人数为666万,试求全市一周内使用滴滴打车超过20分钟的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10kgA级别和20kgB级别茶叶的利润为4000元,销售20kgA级别和10kgB级别茶叶的利润为3500元.
(1)求每千克A级别茶叶和B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200kg用于出口,其中B级别茶叶的进货量不超过A级别茶叶的2倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系. 
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
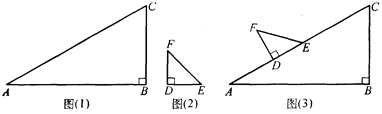
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图(1)、图(2).在图(1)中,∠B=90°,∠A=30°;图(2)中,∠D=90°,∠F=45°.图(3)是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上,移动开始时,点D与点A重合.
(1)△DEF在移动过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com