
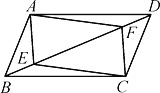
【题目】如图,在□ ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】试题(1)根据平行四边形的性质可得AB=CD,AB∥CD,然后可证明∠ABE=∠CDF,再利用SAS来判定△ABE≌△DCF,从而得出AE=CF.
(2)首先根据全等三角形的性质可得∠AEB=∠CFD,根据等角的补角相等可得∠AEF=∠CFE,然后证明AE∥CF,从而可得四边形AECF是平行四边形.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
 ,
,
∴△ABE≌△DCF(SAS).
∴AE=CF.
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
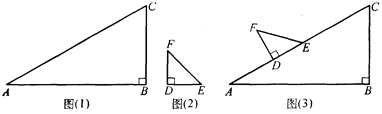
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图(1)、图(2).在图(1)中,∠B=90°,∠A=30°;图(2)中,∠D=90°,∠F=45°.图(3)是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上,移动开始时,点D与点A重合.
(1)△DEF在移动过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于![]() 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形正确的是( )
A. 4x﹣5=3x+2变形得 4x﹣3x=2﹣5
B. ![]() 变形得x=1
变形得x=1
C. 3(x﹣1)=2(x+3)变形得3x﹣1=2x+6
D. ![]() 变形得3x=15
变形得3x=15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 上课时李老师提出这样一个问题:对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,求a的取值范围.
小捷的思路是:原不等式等价于x2﹣2x﹣1>a,设函数y1=x2﹣2x﹣1,y2=a,画出两个函数的图象的示意图,于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围.
请结合小捷的思路回答:
对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,则a的取值范围是.
参考小捷思考问题的方法,解决问题:
关于x的方程x﹣4= ![]() 在0<a<4范围内有两个解,求a的取值范围.
在0<a<4范围内有两个解,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年8月1日是中国人民解放军成立90周年纪念日,某学校团委为此准备举行“学唱红歌”歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱曲目,为此提供代号为A,B,C,D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①、图②所提供的信息,解答下列问题: 
(1)本次抽样调查的学生有名,其中选择曲目代号为A的学生所对应圆心角的度数为;
(2)请将图②补充完整;
(3)若该校共有1800名学生,根据抽样调查的结果估计全校共有多少名学生选择代号为C的曲目为必唱歌曲?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com