
【题目】某商场销售一种夹克和衬衣,夹克每件定价100元,衬衣每件定价50元,商场在开展促销活动期间,向顾客提供两种优惠方案。
方案一:买一件夹克送一件衬衣
方案二:夹克和衬衣均按定价的80%付款
现有顾客要到该商场购买夹克30件,衬衣x件(x>30)
(1)若用方案一购买夹克需付款 元,衬衣需付款(用含x的式子表示) 元,共需付款 元。
若用方案二购买夹克需付款 元,衬衣需付款(用含x的式子表示) 元,共需付款 元。
(2)通过计算说明,购买衬衣多少件时,两种方案付款一样多?
(3)当x=40时,哪种方案更省钱?请说明理由
【答案】(1)3000,50x-1500,50x+1500,2400,40x, 40x+2400;(2)90;(3)方案一更省钱,理由见解析.
【解析】
(1)根据题意直接写出代数式即可.
(2)设购买衬衣![]() 件时,两种方案付款一样多,即可列出方程进行求解,
件时,两种方案付款一样多,即可列出方程进行求解,
(3)把将x=40分别代入两代数式即可求出各款数,即可进行比较.
(1)该商场购买夹克30件,衬衣x件(x>30),用方案一购买夹克需付款3000元,衬衣需付款(50x-1500)元,共需付款(50x+1500)元;
若用方案二购买夹克需付款2400元,衬衣需付款40x元,共需付款(40x+2400)元。
(2)解:设购买衬衣![]() 件时,两种方案付款一样多,
件时,两种方案付款一样多,
根据题意得:50x+1500=40x+2400
解得: x=90
答:购买90件衬衣,两种方案付款一样多。
(3)将x=40代入50x+1500得:50x+1500=3500;将x=40代入40x+2400得:40x+2400=4000;
3500<4000,所以,方案一更省钱。


科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离(结果精确到0.1米,参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣ ![]() x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限内作等边△ABC.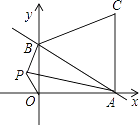
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a, ![]() ),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值.
),请用含a的式子表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)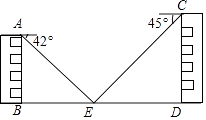
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com