
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需要加密传输,其原理如下:

现将10个数字按图所示排成一个圈,并设置了一种数字信息的加密规则:加密钥匙为“n&3”,“n&3”代表“把明文n换成图中从它开始顺时针跳过3个数字的那个数字”,例如明文是5时,对应的密文为9.若收到的密文是6452,那么通过解密,它对应的明文是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B、C三点表示的数分别为![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)则![]() = ,
= , ![]() = ;
= ;
(2)动点P从A点出发,以每秒10个单位的速度沿数轴向右运动,到达B点停留片刻后立即以每秒6个单位的速度沿数轴返回到A点,共用了6秒;其中从C到B,返回时从B到C(包括在B点停留的时间)共用了2秒.
①求C点表示的数![]() ;
;
②设运动时间为![]() 秒,求
秒,求![]() 为何值时,点P到A、B、C三点的距离之和为23个单位?
为何值时,点P到A、B、C三点的距离之和为23个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:
若二次三项式x2-4x+m有一个因式是x+3,求另一个因式及m的值.
解:设另一个因式为x+a
则x2-4x+m=(x+3)(x+a)=x2+ax+3x+3a=x2+(a+3)x+3a,
∴![]() ∴
∴![]()
∴另一个因式为x-7,m的值为-21.
请依照以上方法解答下面问题:
(1)已知二次三项式x2+3x-k有一个因式是x-5,求另一个因式及k的值;
(2)已知二次三项式2x2+5x+k有一个因式是x+3,求另一个因式及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便居民低碳出行,2015年12月30日,湘潭市公共自行车租赁系统(一期)试运行以来,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出). 
请根据上面的统计图,解答下列问题:
(1)被调查的总人数是人;
(2)公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了多少?
(3)如果该小区共有居民2000人,公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( ![]() )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(
)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( ![]() )海里.
)海里.
(1)分别求出A与C及B与C的距离AC、BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?
(参考数据: ![]() =1.41,
=1.41, ![]() =1.73,
=1.73, ![]() =2.45)
=2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①下午 2 点 10 分时,钟表的时针和分针所成锐角是________;
②如图,射线 OC,OD 在∠AOB 的内部,射线 OM,ON 分别平分∠AOD,∠BOC, 且∠BON=50°,∠AOM=40°,∠COD=30°,则∠AOB 的度数为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠BAC=90°,CD= ![]() BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
(1)如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长; 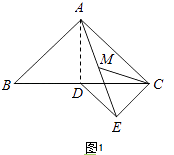
(2)如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证:MN⊥AE; 
(3)如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索 ![]() 的值并直接写出结果.
的值并直接写出结果. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com