
����Ŀ����ͼ��������A��B��C�����ʾ�����ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]()
(1)��![]() = ��
= �� ![]() = ��
= ��
(2)����P��A���������ÿ��10����λ���ٶ������������˶�������B��ͣ��Ƭ�̺�������ÿ��6����λ���ٶ������᷵�ص�A�㣬������6�룻���д�C��B������ʱ��B��C(������B��ͣ����ʱ��)������2����
����C���ʾ����![]() ��
��
�����˶�ʱ��Ϊ![]() �룬��
�룬��![]() Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
���𰸡���1��a=��8��b=12����2��7����3��1.2��1.8��3��4.
�������������������1������ż�η��Լ�����ֵ�ķǸ��Լ������a��b��ֵ��
��2����AC=x��������AC�������˶���ʱΪ6-2=4���з�����⼴�ɣ�
��3����4��������з������ۼ��ɵý�.
�����������1����![]()
��a+8=0��b-12=0��
��ã�a=-8��b=12��
��2����AC=x����������ã�
![]() ��
��
���x=15��
c=��8+15=7��
��3���ٵ�P��A��B��AC���˶�ʱ����t��ʱ����P��A��B��C����ľ���֮��Ϊ23����λ����������ã�
-8+10t+7-10+12-10t=23
��ã�t=1.2
�ڵ�P��A��B��CB���˶�ʱ����t��ʱ����P��A��B��C����ľ���֮��Ϊ23����λ����������ã�
10t+10t-7+12-10t=23
��ã�t=1.8
ͬ���ɵã�t=3��t=4.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6�֣�������С�������һ����
��Ŀ����ͬһƽ���ϣ�����BOA=70������BOC=15������AOC�Ķ�����
�⣺��������ɻ���ͼ��

�ߡ�AOC=��BOA����BOC
=70����15��
=55����
���AOC=55����
��������ʦ������С�������������ᣬ˵�����ɣ������ᣬ�뽫С�����ĵĴ���ָ��������������Ϊ��ȷ�Ľⷨ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC��һ�ŷ���ƽ��ֱ������ϵ�еij�����ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=10 ,OC=8����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E��.
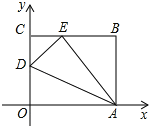
��1����CE��OD�ij���
��2����ֱ��DE�ı���ʽ��
��3��ֱ��y=kx+b��DEƽ�У����������OABC�й�����ʱ��ֱ��д��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����ϣ����Ź�ͼ��Դ���ҹ��Ŵ�����ʱ�ڵġ����顱![]() ͼ1��ʾ
ͼ1��ʾ![]() ��������������ľ����ֳơ��÷������ý������ѧ���ŷ�������������顱����һ�����ס��÷���
��������������ľ����ֳơ��÷������ý������ѧ���ŷ�������������顱����һ�����ס��÷���![]() ͼ2��ʾ
ͼ2��ʾ![]() ��
��
�������ܽᣩ�۲�ͼ1��ͼ2�����ݡ��Ź�ͼ���и�����֮��Ĺ�ϵ�����ǿ����ܽ�����÷�����Ҫ�����������______����ͼ3����һ�����÷�������![]() ______��
______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������һ�������㣺��������������a��b��
�涨a ��![]() �� �磺1��
�� �磺1��![]() .
.
��1����2����5��ֵ��
��2����![]() ��3��8����a��ֵ��
��3��8����a��ֵ��
��3����m��2��x�� n����-1��x����3������xΪ�����������ԱȽϴ�Сm n����������������������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������Ŀ�Ľ�����̣����ش�����.
��![]() ,��x2+y2��ֵ.
,��x2+y2��ֵ.
�⣺��![]() ����ԭʽ�ɻ�Ϊa2-8a+16=0����(a-4)2=0������a=4.
����ԭʽ�ɻ�Ϊa2-8a+16=0����(a-4)2=0������a=4.
��(x2+y2)2=4����x2+y2=��2.
��1�������ԭ����___________________________________
��2��������ȷ�Ľ���Ϊ_________________________________
��3������![]() ���ķ���������Ԫ������������Ϊ���Ŀ��.��������Ԫ������(x+y)2-14(x+y)+49��ʽ�ֽ�.
���ķ���������Ԫ������������Ϊ���Ŀ��.��������Ԫ������(x+y)2-14(x+y)+49��ʽ�ֽ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ӳֽ�������������ӣ�ÿ��������3�����β����2���������ε�����ɡ�Ӳֽ������ͼ���ַ�ʽ�ü����ü���߽��ϲ������ã�
A��������6�����棻 B��������4�������5�����档

����19��Ӳֽ�壬�ü�ʱ![]() ����A������������B������
����A������������B������
��1����![]() �Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
�Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
��2�����ü����IJ���͵���ǡ��ȫ�����꣬���������ٸ����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=�� ![]() x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0��
x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0��
��1���������ߵĽ���ʽ����Գ��ᣮ
��2������AC��BC�����жϡ�AOC���COB�Ƿ����ƣ���˵�����ɣ�
��3��MΪ��������BC֮���һ�㣬NΪ�߶�BC�ϵ�һ�㣬��MN��y�ᣬ��MN�����ֵ��
��4���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��AB����һ��P����M��N�ֱ�Ϊ�߶�PA��PB���е㣬AB��14.
(1)����P���߶�AB�ϣ���AP��8�����߶�MN�ij��ȣ�
(2)����P��ֱ��AB���˶�����AP��x��BP��y����ֱ�����������ʱMN�ij��ȣ�
�ٵ�P��AB֮��(��A��B)��
�ڵ�P��A��ߣ�
�۵�P��B�ұߣ�
�㷢����ʲô���ɣ�
(3)��ͼ2������CΪ�߶�AB���е㣬��P���߶�AB���ӳ����ϣ����н��ۣ���![]() ��ֵ���䣻��
��ֵ���䣻��![]() ��ֵ���䣬��ѡ��һ����ȷ�Ľ��۲�����ֵ��
��ֵ���䣬��ѡ��һ����ȷ�Ľ��۲�����ֵ��
ͼ1
![]() ,
,
ͼ2
![]() ,
,
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com