
����Ŀ����ͼ1��ֱ��AB����һ��P����M��N�ֱ�Ϊ�߶�PA��PB���е㣬AB��14.
(1)����P���߶�AB�ϣ���AP��8�����߶�MN�ij��ȣ�
(2)����P��ֱ��AB���˶�����AP��x��BP��y����ֱ�����������ʱMN�ij��ȣ�
�ٵ�P��AB֮��(��A��B)��
�ڵ�P��A��ߣ�
�۵�P��B�ұߣ�
�㷢����ʲô���ɣ�
(3)��ͼ2������CΪ�߶�AB���е㣬��P���߶�AB���ӳ����ϣ����н��ۣ���![]() ��ֵ���䣻��
��ֵ���䣻��![]() ��ֵ���䣬��ѡ��һ����ȷ�Ľ��۲�����ֵ��
��ֵ���䣬��ѡ��һ����ȷ�Ľ��۲�����ֵ��
ͼ1
![]() ,
,
ͼ2
![]() ,
,
���𰸡���1��7.��2���ٵ�P��AB֮�䣬MN��![]() (x��y)���ڵ�P��A��ߣ�MN��
(x��y)���ڵ�P��A��ߣ�MN��![]() (y��x)���۵�P��BA���ӳ����ϣ�MN��
(y��x)���۵�P��BA���ӳ����ϣ�MN��![]() (x��y)����3��ѡ��ڢ�
(x��y)����3��ѡ��ڢ�![]() ��
��![]() (�ڱ仯)����
(�ڱ仯)����![]() ��2
��2
��������
��1����AP��8�ҵ�M��AP���е���MP��![]() AP��4��BP=AB��AP��6�����ɵ�N��PB���е��֪PN��
AP��4��BP=AB��AP��6�����ɵ�N��PB���е��֪PN��![]() PB��3����MN��MP��PN��7��
PB��3����MN��MP��PN��7��
��2�������߶��е�����ʣ��ɵ�MP��NP�ı���ʽ���ٸ����߶εĺͲ��ϵ�ֱ�������������MN�ij��ȼ��ɣ�
��3�������߶εĺͲ�ֱ�ɵ�PA-PB=AB��PA+PB=PC+AC+PC-BC=2PC���ٸ��ݷ�ʽ�����ʼ����ж�.
�⣺(1)��AP��8����M��AP���е㣬
��MP��![]() AP��4��
AP��4��
��BP��AB��AP��6.
������N��PB���е㣬
��PN��![]() PB��3��
PB��3��
��MN��MP��PN��7.
(2)����P��AB֮�䣬MN��MP��PN=![]() =
=![]() (x��y)��
(x��y)��
����P��A��ߣ�MN��PN-MP=![]() -
-![]() =
=![]() (y��x)��
(y��x)��
����P��BA���ӳ����ϣ�MN=MP-PN=![]() -
-![]() ==
==![]() (x��y)��
(x��y)��
(3)ѡ����.
��![]() ������PC���Ȳ��̶�����
������PC���Ȳ��̶�����![]() ��ֵ�DZ仯����
��ֵ�DZ仯����
��![]() ���Ƕ�ֵ��
���Ƕ�ֵ��
����ȷ�Ľ�����������ֵΪ2.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A��B��C�����ʾ�����ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]()
(1)��![]() = ��
= �� ![]() = ��
= ��
(2)����P��A���������ÿ��10����λ���ٶ������������˶�������B��ͣ��Ƭ�̺�������ÿ��6����λ���ٶ������᷵�ص�A�㣬������6�룻���д�C��B������ʱ��B��C(������B��ͣ����ʱ��)������2����
����C���ʾ����![]() ��
��
�����˶�ʱ��Ϊ![]() �룬��
�룬��![]() Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� 2 �� 10 ��ʱ���ӱ���ʱ��ͷ������������________��
����ͼ������ OC��OD �ڡ�AOB ���ڲ������� OM��ON �ֱ�ƽ�֡�AOD����BOC�� �ҡ�BON=50�㣬��AOM=40�㣬��COD=30�㣬���AOB �Ķ���Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��3��32��33��34��35��36��37��38��ֵʱ���������֣��ӵڶ���������ÿһ����������ǰһ��������3�������������裺S��1��3��32��33��34��35��36��37��38����
Ȼ���ڢ�ʽ�����߶���3����3S��3��32��33��34��35��36��37��38��39��
�����ٵã�3S��S��39��1����2S��39��1��
����S��![]() .
.
�ó��𰸺����Խ���ź��룺�������3��������ĸa(a��0��a��1)���ܷ����1��a��a2��a3��a4������a2 017��ֵ���������������ȷ����__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ
12=1= ![]() ��1��2����2+1��
��1��2����2+1��
12+22= ![]() ��2��3����4+1��
��2��3����4+1��
12+22+32= ![]() ��3��4����6+1��
��3��4����6+1��
12+22+32+42= ![]() ��4��5����8+1����
��4��5����8+1����
�����Ʋ�12+22+32+��+n2= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A=2x2+ax��5y+b��B=bx2��![]() x��
x��![]() y��3��
y��3��
��1����3A����4A��2B����ֵ��
��2����xȡ������ֵ��A��2B��ֵ��һ����ֵʱ����a+![]() A������2b+
A������2b+![]() B����ֵ��
B����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵ���ֱ�������Σ���BAC=90�㣬CD= ![]() BC��DE��CE��DE=CE������AE����M��AE���е㣮
BC��DE��CE��DE=CE������AE����M��AE���е㣮
��1����ͼ1������D��BC���ϣ�����CM����AB=4ʱ����CM�ij��� 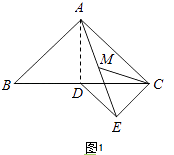
��2����ͼ2������D�ڡ�ABC���ڲ�������BD����N��BD�е㣬����MN��NE����֤��MN��AE�� 
��3����ͼ3����ͼ2�еġ�CDE�Ƶ�C��ʱ����ת��ʹ��BCD=30�㣬����BD����N��BD�е㣬����MN��̽�� ![]() ��ֵ��ֱ��д�������
��ֵ��ֱ��д������� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ڸۿ�P�ı�ƫ��60�㷽��ۿ�56�����A���������Ӹۿ�P�������ر�ƫ��45�㷽������ʻ��ۿ�P��4Сʱ�������С������������������ĺ����ٶȣ�����ȷ��0.1����/ʱ���ο����ݣ� ![]() ��1.41��
��1.41�� ![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��ֱ��y����![]() x��3��������ֱ��ڵ�A��B����ֱ��y��x���ڵ�C���߶�OA�ϵĵ�Q��ÿ��1����λ���ٶȴӵ�O�������A�������˶����˶�ʱ��Ϊt�룬����CQ.
x��3��������ֱ��ڵ�A��B����ֱ��y��x���ڵ�C���߶�OA�ϵĵ�Q��ÿ��1����λ���ٶȴӵ�O�������A�������˶����˶�ʱ��Ϊt�룬����CQ.
(1)�����C�����ꣻ
(2)����OQC�ǵ���ֱ�������Σ���t��ֵΪ________��
(3)��CQƽ����OAC���������ֱ��CQ��Ӧ�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com