
【题目】如图6,在平面直角坐标系中,一次函数![]() =
=![]() +1的图象交
+1的图象交![]() 轴于点D,与反比例函数
轴于点D,与反比例函数![]() =
=![]() 的图象在第一象限相交于点A.过点A分别作
的图象在第一象限相交于点A.过点A分别作![]() 轴
轴![]() 轴的垂线,垂足为点BC.
轴的垂线,垂足为点BC.
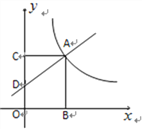
(1)点D的坐标为 ;
(2)当AB=4AC时,求![]() 值;
值;
(3)当四边形OBAC是正方形时,直接写出四边形ABOD与△ACD面积的比.
【答案】(1) D(0,1); (2)![]() ;(3)5:3.
;(3)5:3.
【解析】分析:
(1)在y=kx+1中,由x=0可得y=1,由此可得点D的坐标为(0,1);
(2)设点A的坐标为(a,b),由题意可得b=4a,代入反比例函数的解析式![]() 即可解得a的值,从而得到点A的坐标,把所得坐标代入y=kx+1中即可求得k的值;
即可解得a的值,从而得到点A的坐标,把所得坐标代入y=kx+1中即可求得k的值;
(3)由题意可设点A的坐标为(m,m),代入![]() 中,求得m的值,即可得到此时点A的坐标,结合点D的坐标即可求得四边形ABOD和△ACD的面积,从而可求得两个图形的面积比.
中,求得m的值,即可得到此时点A的坐标,结合点D的坐标即可求得四边形ABOD和△ACD的面积,从而可求得两个图形的面积比.
详解:
(1)∵在y=kx+1中,当x=0时,y=1,
∴点D的坐标为:(0,1);
(2)设点A(a,b),
∵点A在第一象限,
∴a与b均大于0,即AB=b,AC=a,
∵AB=4AC,
∴得b=4a,
代入反比例函数解析式![]() ,得
,得![]() ,
,
解得:a=2或a=-2(不合题意,舍去),
∴A的坐标为A(2,8),
代入一次函数y=kx+1得:8=2k+1,
解得:![]() ;
;
(3)∵四边形OBAC是正方形,
∴OB=AB,
∴可设点A的坐标为(m,m),
代入![]() 得:
得:![]() ,解得m=4或m=-4(不合题意,舍去),
,解得m=4或m=-4(不合题意,舍去),
∴点A的坐标为(4,4),
∴AB=OB=AC=OC=4,
又∵点D的坐标为(0,1),
∴OD=1,CD=3,
∴S△ACD=![]() AC·CD=6,S四边形OBAD=
AC·CD=6,S四边形OBAD=![]() (AB+OD)·OB=10,
(AB+OD)·OB=10,
∴S四边形OBAD:S△ACD=5:3.


科目:初中数学 来源: 题型:
【题目】前不久在台湾抗震救灾中,某地将甲、乙两个仓库的粮食全部转移到A、B两个仓库.甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A,B两库的路程和运费如下表:
路程(km) | 运费(元/吨km) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)函数关系式.
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】厉害了,我的国!2018年10月24日,珠港澳大桥建成通车,成了世界瞩目的焦点.这座连接中国珠海、香港、澳门三座城市,全长55公里,投资1269亿元经过6年筹备与9年建设的跨海大桥,创造了400多项专利和七项世界之最,被誉为世界的第七大奇迹,是中国科技实力的伟大展现,令全球华人倍感骄傲与自豪.用科学记数法表示大桥的投资款正确的是( )
A.12.69×![]() 亿元B.1.269×
亿元B.1.269×![]() 元
元
C.1.269×![]() 元D.1.269×
元D.1.269×![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.

(1)求∠DOE和∠DOF的度数;
(2)若∠DOC=3∠COF,求∠AOC的度数;
(3)求∠BOF+∠DOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=﹣x+4于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.

(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() =
=![]() (
(![]() ≠0)与
≠0)与![]() 轴交于AB两点,与
轴交于AB两点,与![]() 轴交于C点,其对称轴为
轴交于C点,其对称轴为![]() =1,且A(-1,0)C(0,2).
=1,且A(-1,0)C(0,2).
(1)直接写出该抛物线的解析式;
(2)P是对称轴上一点,△PAC的周长存在最大值还是最小值?请求出取得最值(最大值或最小值)时点P的坐标;
(3)设对称轴与![]() 轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交
轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交![]() 轴于点E.连接PDPE.若CD的长为
轴于点E.连接PDPE.若CD的长为![]() ,△PDE的面积为S,求S与
,△PDE的面积为S,求S与![]() 之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时
之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com