
����Ŀ���Ķ����ϣ�����̵Ľⷨ�����һԪһ�η��̣����ݵ�ʽ�Ļ������ʣ��ѷ���ת��Ϊx=a����ʽ.����Ԫһ�η����飬����ת��ΪһԪһ�η������⣻���Ƶģ������Ԫһ�η����飬����ת��Ϊ���Ԫһ�η�����.���һԪ���η��̣�����ת��Ϊ����һԪһ�η�������.����ʽ���̣�����ת��Ϊ��ʽ�������⣬���ڡ�ȥ��ĸ�����ܲ������������Խ��ʽ���̱������.����̵Ľⷨ������ͬ������������һ����ͬ�Ļ�����ѧ˼��ת������δ֪ת��Ϊ��֪.�á�ת��������ѧ˼�룬���ǻ����Խ�һЩ�µķ���.���磬һԪ���η���![]() ������ͨ����ʽ�ֽ����ת��Ϊ
������ͨ����ʽ�ֽ����ת��Ϊ![]() ���ɵ�
���ɵ�![]() ������x=0��x+2=0��x-1=0�����Է��̣�
������x=0��x+2=0��x-1=0�����Է��̣�![]() �Ľ���x1=0��x2=-2��x3=1��
�Ľ���x1=0��x2=-2��x3=1��
��1�����⣺�á�ת����˼����![]() �Ľ�
�Ľ�
��2��Ӧ�ã���ͼ����֪���β�ƺABCD�ij�AD=8m����AB=3m��С����һ����Ϊ10m�����ӵ�һ�˹̶��ڵ�B���ز�ƺ����BA��AD�ߵ���P�����ѳ���PB����ֱ���̶��ڵ�P��Ȼ���ز�ƺ����PD��DC�ߵ���C�����ѳ���ʣ�µ�һ����ֱ����������һ��ǡ�����ڵ�C.��AP�ij�.
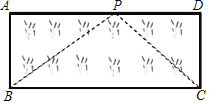
���𰸡���1��3����2��AP=4m��
��������
��1������ƽ��������������ת��Ϊ��ʽ���̣���⣬ע�������
��2����AP�ij�Ϊxm�����ݹ��ɶ�����BP+CP=10�����г����̣����ڷ��̺��и��ţ�����ƽ��������������ת��Ϊ��ʽ���̣���⣬
�⣺��1��![]()
���̵�����ƽ������2x+3=x2��
���x1=-1����ȥ����x2=3��
��x=-1ʱ��![]() =
=![]() =1��-1��
=1��-1��
����-1����ԭ���̵Ľ⣮
���Է���![]() �Ľ���x=3��
�Ľ���x=3��
��2����AP=x����DP=8-x��
��BP+CP=10��
���ݹ��ɶ�����BP=![]() ��CP=
��CP=![]()
��![]()
![]()
����ƽ������![]()
��������![]()
����ƽ������������x2-8x+16=0
����x-4��2=0
����x=4��
�����飬x=4�Ƿ��̵Ľ⣮
��AP�ij�Ϊ4m��
�ʴ�Ϊ����1��3����2��AP=4m��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
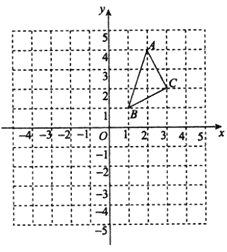
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��A��B��C�����ڸ���ϣ�
(1)������ABC����x��ԳƵġ�A1B1C1����д����A1��B1��C1�����ꣻ
(2)������ABC����ԭ��O�ԳƵġ�A2B2C2����д����A2��B2��C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��BC��CD�ֱ����O������E��F��G����AB��CD��OB=6cm��OC=8cm����
��1����BOC�Ķ�����
��2��BE+CG�ij���
��3����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
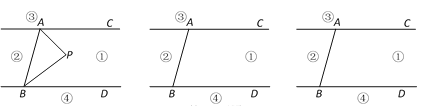
����Ŀ����ͼ��ֱ��AC��BD������AB��ֱ��AC��BD���߶�AB��ƽ��ֳɢ١��ڡ��ۡ����ĸ����֣��涨�����ϸ��㲻�����κβ��֣�������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ�(��ʾ���й����˵�������غϵ���������ɵĽ���0��)
(1)������P���ڵڢٲ���ʱ���С�APB����PAC����PBD����˵�����ɣ�
(2)������P���ڵڢڲ���ʱ����APB����PAC����PBD�Ƿ������������������д����PAC����APB����PBD�����ǵĵ�����ϵ(����˵������)��
(3)������P�ڵڢ۲���ʱ��̽����PAC����APB����PBD֮��Ĺ�ϵ��д���㷢�ֵ�һ������������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
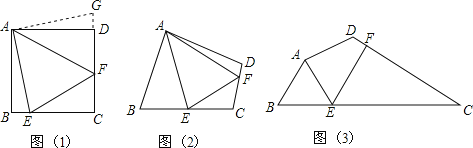
����Ŀ�����⣺��ͼ��1������E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF��45�������ж�BE��EF��FD֮���������ϵ��
������֤����С�ϰ���ABE�Ƶ�A��ʱ����ת90������ADG���Ӷ�����EF��BE+FD����������ͼ��1��֤���������ۣ�
��������꣩��ͼ��2�����ı���ABCD�У���BAD��90����AB��AD����B+��D��180������E��F�ֱ��ڱ�BC��CD�ϣ���EAF���BAD������ ����ϵʱ������EF��BE+FD��
��̽��Ӧ�ã���ͼ��3������ij����ͬһˮƽ���ϣ�����ͨ��Χ���ı���ABCD����֪AB��AD��80�ף���B��60������ADC��120������BAD��150������·BC��CD�Ϸֱ��о���E��F����EAF��75����AE��AD��DF��40��![]() ��1���ף���Ҫ��E��F֮����һ����ֱ��·����������·EF�ij������ȡ�������ο����ݣ�
��1���ף���Ҫ��E��F֮����һ����ֱ��·����������·EF�ij������ȡ�������ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ˣ��ҵĹ�!2018��10��24�գ���۰Ĵ��Ž���ͨ��������������Ŀ�Ľ��㣮���������й��麣����ۡ������������У�ȫ��55���Ͷ��1269��Ԫ����6��ﱸ��9�꽨��Ŀ纣���ţ�������400����ר������������֮�����Ϊ����ĵ��ߴ��漣�����й��Ƽ�ʵ����ΰ��չ�֣���ȫ���˱��н������Ժ����ÿ�ѧ��������ʾ���ŵ�Ͷ�ʿ���ȷ����( )
A.12.69��![]() ��ԪB.1.269��
��ԪB.1.269��![]() Ԫ
Ԫ
C.1.269��![]() ԪD.1.269��
ԪD.1.269��![]() Ԫ
Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϣ���![]() ��ʾ
��ʾ![]() ����
����![]() ��ʾ
��ʾ![]() ����
����![]() ��ʾ
��ʾ![]() .����
.����![]() �ӵ�
�ӵ�![]() ��������������������ÿ��
��������������������ÿ��![]() ����λ���ٶ������˶�;ͬʱ������
����λ���ٶ������˶�;ͬʱ������![]() �ӵ�
�ӵ�![]() �����������Ḻ������ÿ��
�����������Ḻ������ÿ��![]() ����λ���ٶ������˶�.���˶�ʱ��Ϊ
����λ���ٶ������˶�.���˶�ʱ��Ϊ![]() ��.
��.
(1)��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() ��������?������
��������?������![]() ����Ӧ�����Ƕ���?
����Ӧ�����Ƕ���?
(2)�ڵ�![]() �������
�������![]() ֮ǰ����
֮ǰ����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ����
����![]() �ľ������
�ľ������![]() ����
����![]() �ľ������;
�ľ������;
(3)�ڵ�![]() �����˶��Ĺ����У�
�����˶��Ĺ����У�![]() ��
��![]() ���е㣬�ڵ�
���е㣬�ڵ�![]() �����
�����![]() ֮ǰ����
֮ǰ����![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪֱ��AB��һ�㣬����O��ֱ��OC����֪��AOC��90��������ODƽ�֡�AOC������OEƽ�֡�BOC������OFƽ�֡�DOE��

��1�����DOE�͡�DOF�Ķ�����
��2������DOC=3��COF�����AOC�Ķ�����
��3�����BOF+��DOC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=![]() ��ͼ����һ�κ���y=kx+m��ͼ���ཻ�ڵ�A��2��1����
��ͼ����һ�κ���y=kx+m��ͼ���ཻ�ڵ�A��2��1����
��1���ֱ���������������Ľ���ʽ��
��2����xȡʲô��Χʱ������������ֵ����0��
��3����һ�κ����뷴����������һ����ΪB����������Ϊ��4����xȡʲô��Χʱ������������ֵ����һ�κ�����ֵ��
��4�����жϵ�P����1��5������x��ĶԳƵ�P���Ƿ���һ�κ���y=kx+m��ͼ���ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com