
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

【答案】(1)∠BOC=90°;(2)BE+CG =10cm;(3)OF=4.8cm.
【解析】试题分析:(1)连接OF,根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;再根据平行线性质得到∠BOC为直角;
(2)进而由切线长定理即可得到BE+CG的长;
(3)由勾股定理可求得BC的长,最后由三角形面积公式即可求得OF的长.
试题解析:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°;
(2)∵OB=6cm,OC=8cm,
∴BC=10cm,
∴BE+CG=BC=10cm.
(3)OF=4.8



 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】“元旦”期间,某文具店购进 ![]() 只两种型号的文具进行销售,其进价和售价如表:
只两种型号的文具进行销售,其进价和售价如表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用 ![]() 元可以购进A,B两种型号的文具各多少只?
元可以购进A,B两种型号的文具各多少只?
(2)在(![]() )的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过
)的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过 ![]() ?请你说明理由.
?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(8,0)及在第一象限的动点P(x,y),且x+y=10,设△OPA的面积为S
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)求S=12时P点坐标;
(4)画出函数S的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BOC=2∠AOC,OD平分∠AOB,∠BOE=90°,若∠AOC=40°,则∠DOE的度数等于( )
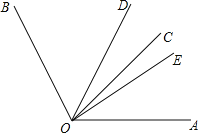
A.20°B.25°C.30°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法:求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,可得
,可得![]() ,所以x=0或x+2=0或x-1=0,所以方程:
,所以x=0或x+2=0或x-1=0,所以方程:![]() 的解是x1=0,x2=-2,x3=1;
的解是x1=0,x2=-2,x3=1;
(1)问题:用“转化”思想求方程![]() 的解
的解
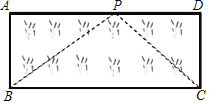
(2)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com