
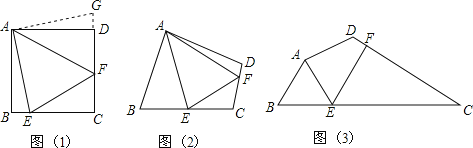
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
(发现证明)小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(类比引申)如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
(探究应用)如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,∠EAF=75°且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】【发现证明】见解析;【类比引申】∠BAD=2∠EAF. 【探究应用】这条道路EF的长约为109米.
【解析】
[发现证明]根据旋转的性质可以得到△ADG≌△ABE,则GF=BE+DF,只要再证明△AFG≌△AFE即可.
[类比引申]延长CB至M,使BM=DF,连接AM,证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案;
[探究应用]利用等边三角形的判定与性质得到△ABE是等边三角形,则BE=AB=80米.把△ABE绕点A逆时针旋转150°至△ADG,只要再证明∠BAD=2∠EAF即可得出EF=BE+FD.
[发现证明]根据旋转的性质可以得到△ADG≌△ABE,则GF=BE+DF,只要再证明△AFG≌△AFE即可.
[类比引申]∠BAD=2∠EAF.如图(2),延长CB至M,使BM=DF,连接AM,
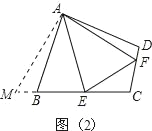
证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案;
[探究应用]如图3,把△ABE绕点A逆时针旋转150°至△ADG,连接AF.
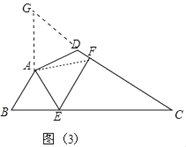
∵∠BAD=150°,∠DAE=90°,
∴∠BAE=60°.
又∵∠B=60°,
∴△ABE是等边三角形,
∴BE=AB=80米.
根据旋转的性质得到:∠ADG=∠B=60°,
又∵∠ADF=120°,
∴∠GDF=180°,即点G在CD的延长线上.
易得,△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAG=∠BAD=150°,∠FAE=75°
∴∠GAF=∠FAE,
在△GAF和△FAE中,
AG=AE,∠GAF=∠FAE,AF=AF,
∴△AFG≌△AFE(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴EF=BE+DF=80+40(![]() ﹣1)≈109(米),
﹣1)≈109(米),
即这条道路EF的长约为109米.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B旋转90°,分别得到线段B P1,B P2,称点P1,P2为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图.
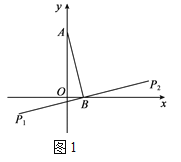
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(-2,0)时,点A关于点B的“伴随点”的坐标分别为 ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
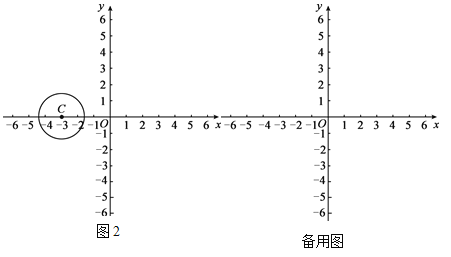
(2)如图2,点C的坐标为(-3,0),以C为圆心, ![]() 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BOC=2∠AOC,OD平分∠AOB,∠BOE=90°,若∠AOC=40°,则∠DOE的度数等于( )
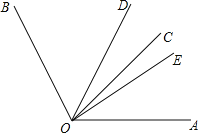
A.20°B.25°C.30°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法:求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,可得
,可得![]() ,所以x=0或x+2=0或x-1=0,所以方程:
,所以x=0或x+2=0或x-1=0,所以方程:![]() 的解是x1=0,x2=-2,x3=1;
的解是x1=0,x2=-2,x3=1;
(1)问题:用“转化”思想求方程![]() 的解
的解
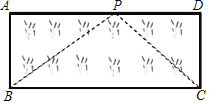
(2)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
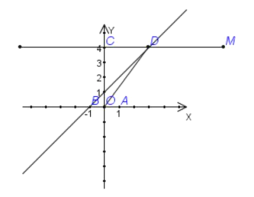
【题目】在直角坐标平面内,![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 轴. 点
轴. 点![]() 与点
与点![]() 关于原点对称,直线
关于原点对称,直线![]() (
(![]() 为常数)经过点
为常数)经过点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)在![]() 轴上有一点
轴上有一点![]() ,使
,使![]() 的面积为
的面积为![]() ,求
,求![]() 点的坐标;
点的坐标;
(3)在![]() 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点![]() ,使得
,使得![]() 为等腰三角形,若存在,求出点
为等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
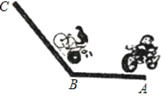
【题目】如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
查看答案和解析>>
科目:初中数学 来源: 题型:
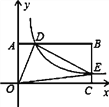
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )
A. 6 B. 9 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com