
ЁОЬтФПЁПШчЭМЃЌжБЯпABНЛxжсгкЕуBЃЈ2ЃЌ0ЃЉЃЌНЛyжсгкЕуAЃЈ0ЃЌ2ЃЉЃЌжБЯпDMЁЭxжсе§АыжсгкЕуMЃЌНЛЯпЖЮABгкЕуCЃЌDM=3ЃЌСЌНгDAЃЌЁЯDAC=90ЁуЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЧѓDЕузјБъМАЙ§OЁЂDЁЂBШ§ЕуЕФХзЮяЯпНтЮіЪНЃЎ
ЃЈ3ЃЉШєЕуPЪЧЯпЖЮOBЩЯЕФЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпНЛABгкFЃЌНЛЃЈ2ЃЉжаХзЮяЯпгкEЃЌСЌCEЃЌЪЧЗёДцдкPЪЙЁїBPFгыЁїFCEЯрЫЦЃПШєДцдкЃЌЧыЧѓГіPЕузјБъЃЛШєВЛДцдкЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉжБЯпABЕФНтЮіЪНЮЊy=Љx+2ЃЛЃЈ2ЃЉDЕузјБъЪЧЃЈ1ЃЌ3ЃЉЃЌХзЮяЯпЕФНтЮіЪНЮЊy=Љ3xЃЈxЉ2ЃЉЃЛЃЈ3ЃЉPЃЈ![]() ЃЌ0ЃЉЃЛЃЈ
ЃЌ0ЃЉЃЛЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФХаЖЈгыаджЪЃЌПЩЕУDЕузјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉИљОнЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЃЌПЩЕУEЕузјБъЃЌИљОнЕуЕФзјБъТњзуКЏЪ§НтЮіЪНЃЌПЩЕУEЕузјБъЃЌПЩЕУPЕузјБъЃЎ
ЪдЬтНтЮіЃК(1)ЩшжБЯпABЕФНтЮіЪНЮЊy=kx+bЃЌНЋA.BЕузјБъДњШыКЏЪ§НтЮіЪНЃЌЕУ
![]() НтЕУ
НтЕУ![]()
жБЯпABЕФНтЮіЪНЮЊy=x+2ЃЛ
(2)ШчЭМ1ЃЌ
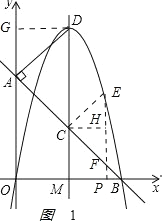
Й§DзїDGЁЭyжсЃЌДЙзуЮЊGЃЌЁпOA=OB=2ЃЌ
ЁрЁїOABЪЧЕШбќжБНЧШ§НЧаЮЁЃ
ЁпADЁЭAB, ![]()
МДЁїADGЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрDG=AG=OGOA=DMOA=32=1ЃЌ
ЁрDЕузјБъЪЧ(1,3)ЃЛ
ЩшХзЮяЯпЕФНтЮіЪНЮЊy=ax(x2)ЃЌНЋDЕузјБъДњШыЃЌЕУ
aЁС1ЁС(12)=3,НтЕУa=3,ХзЮяЯпЕФНтЮіЪНЮЊy=3x(x2)ЃЛ
(3)гЩ(2)ЕУ![]() дђ
дђ![]() ЩшP(x,0)ЃЌMP=x1ЃЌPB=2xЃЌ
ЩшP(x,0)ЃЌMP=x1ЃЌPB=2xЃЌ
ЂйЕБ![]() ЪБ,ЁїBPFЁзЁїFCEЃЌ
ЪБ,ЁїBPFЁзЁїFCEЃЌ
Й§CзїCHЁЭEF, ![]() МДEF=2CH=MPЃЌ
МДEF=2CH=MPЃЌ
ЁрPE=PF+EF=BP+2MP=2x+2(x1)=x,МДE(x,x).
НЋEЕузјБъДњШыХзЮяЯпЃЌЕУ
x=3x(x2)ЃЌ
НтЕУ![]() ЃЈВЛЗћКЯЬтвт,ЩсЃЉ
ЃЈВЛЗћКЯЬтвт,ЩсЃЉ![]() ,МД
,МД![]()
ЂкШчЭМ2ЃЌ
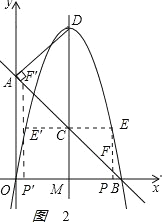
ЕБ![]() ЪБЃЌЁїCEFЁЂЁїBPFЮЊЕШбќжБНЧШ§НЧаЮЃЌPE=MC=1ЃЌ
ЪБЃЌЁїCEFЁЂЁїBPFЮЊЕШбќжБНЧШ§НЧаЮЃЌPE=MC=1ЃЌ
ЁрE(x,1)ЃЌ
НЋEЕузјБъДњШыКЏЪ§НтЮіЪНЃЌЕУ
3x(x2)=1ЃЌ
НтЕУ![]()
ДЫЪБ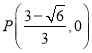 Лђ
Лђ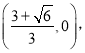
злЩЯЫљЪіЃК ![]()
 Лђ
Лђ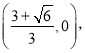



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЈЙ§бЇЯАОјЖджЕ,ЮвУЧжЊЕР![]() ЕФМИКЮвтвхЪЧЪ§жсЩЯБэЪОЪ§
ЕФМИКЮвтвхЪЧЪ§жсЩЯБэЪОЪ§![]() дкЪ§жсЩЯЕФЖдгІЕугыдЕуЕФОрРы,ШчЃК
дкЪ§жсЩЯЕФЖдгІЕугыдЕуЕФОрРы,ШчЃК![]() БэЪО
БэЪО![]() дкЪ§жсЩЯЕФЖдгІЕуЕНдЕуЕФОрРы.
дкЪ§жсЩЯЕФЖдгІЕуЕНдЕуЕФОрРы.![]() ,МД
,МД![]() БэЪО
БэЪО![]() ЁЂ
ЁЂ![]() дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРы,РрЫЦЕФ,
дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРы,РрЫЦЕФ,![]() ЃЌМД
ЃЌМД![]() БэЪО
БэЪО![]() ЁЂ
ЁЂ![]() дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРыЃЛвЛАуЕиЃЌЕу
дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРыЃЛвЛАуЕиЃЌЕу![]() ЃЌ
ЃЌ![]() дкЪ§жсЩЯЗжБ№БэЪОЪ§
дкЪ§жсЩЯЗжБ№БэЪОЪ§![]() ЁЂ
ЁЂ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЃЌ
ЃЌ![]() жЎМфЕФОрРыПЩБэЪОЮЊ
жЎМфЕФОрРыПЩБэЪОЮЊ![]() .
.
ЧыИљОнОјЖджЕЕФМИКЮвтвхВЂНсКЯЪ§жсНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЪ§жсЩЯБэЪО![]() КЭ
КЭ![]() ЕФСНЕужЎМфЕФОрРыЪЧ___ЃЛЪ§жсЩЯ
ЕФСНЕужЎМфЕФОрРыЪЧ___ЃЛЪ§жсЩЯ![]() ЁЂ
ЁЂ![]() СНЕуЕФОрРыЮЊ
СНЕуЕФОрРыЮЊ![]() ЃЌЕу
ЃЌЕу![]() БэЪОЕФЪ§ЪЧ
БэЪОЕФЪ§ЪЧ![]() ЃЌдђЕу
ЃЌдђЕу![]() БэЪОЕФЪ§ЪЧ___.
БэЪОЕФЪ§ЪЧ___.
ЃЈ2ЃЉЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкЪ§жсЩЯЗжБ№БэЪОЪ§
дкЪ§жсЩЯЗжБ№БэЪОЪ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ,ФЧУД
,ФЧУД![]() ЕНЕу
ЕНЕу![]() .Еу
.Еу![]() ЕФОрРыжЎКЭПЩБэЪОЮЊ_ (гУКЌОјЖджЕЕФЪНзгБэЪО)ЃЛШє
ЕФОрРыжЎКЭПЩБэЪОЮЊ_ (гУКЌОјЖджЕЕФЪНзгБэЪО)ЃЛШє![]() ЕНЕу
ЕНЕу![]() .Еу
.Еу![]() ЕФОрРыжЎКЭгазюаЁжЕЃЌдђ
ЕФОрРыжЎКЭгазюаЁжЕЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ_ __.
ЕФШЁжЕЗЖЮЇЪЧ_ __.
ЃЈ3ЃЉ![]() ЕФзюаЁжЕЮЊ_ __.
ЕФзюаЁжЕЮЊ_ __.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбвЛИіжБНЧШ§НЧаЮACBЃЈЁЯACB=90ЁуЃЉШЦзХЖЅЕуBЫГЪБеыа§зЊ60ЁуЃЌЪЙЕУЕуCа§зЊЕНABБпЩЯЕФвЛЕуDЃЌЕуAа§зЊЕНЕуEЕФЮЛжУЃЎFЃЌGЗжБ№ЪЧBDЃЌBEЩЯЕФЕуЃЌBF=BGЃЌбгГЄCFгыDGНЛгкЕуHЃЎ

ЃЈ1ЃЉЧѓжЄЃКCF=DGЃЛ
ЃЈ2ЃЉЧѓГіЁЯFHGЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
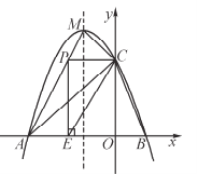
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЌЧвДЫХзЮяЯпЕФЖЅЕузјБъЮЊMЃЈ-1ЃЌ4ЃЉ.
жсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЌЧвДЫХзЮяЯпЕФЖЅЕузјБъЮЊMЃЈ-1ЃЌ4ЃЉ.
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуDЮЊвбжЊХзЮяЯпЖдГЦжсЩЯЕФШЮвтвЛЕуЃЌЕБЁїACDУцЛ§ЕШгк6ЪБЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉЕуPдкЯпЖЮAMЩЯЃЌЕБPCгыyжсДЙжБЪБЃЌЙ§ЕуPзї![]() жсЕФДЙЯпЃЌДЙзуЮЊEЃЌНЋЁїPCEбижБЯпCBЗелЃЌЪЙЕуPЕФЖдгІЕуP'гыPЁЂEЁЂCДІдкЭЌвЛЦНУцФкЃЌЧыЧѓГіP'зјБъЃЌВЂХаЖЯЕуP'ЪЧЗёдкХзЮяЯпЩЯ.
жсЕФДЙЯпЃЌДЙзуЮЊEЃЌНЋЁїPCEбижБЯпCBЗелЃЌЪЙЕуPЕФЖдгІЕуP'гыPЁЂEЁЂCДІдкЭЌвЛЦНУцФкЃЌЧыЧѓГіP'зјБъЃЌВЂХаЖЯЕуP'ЪЧЗёдкХзЮяЯпЩЯ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
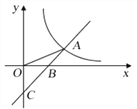
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсНЛгкЕуCЃЌгы
жсНЛгкЕуCЃЌгы![]() жсНЛгкЕуBЃЌгыЗДБШР§КЏЪ§
жсНЛгкЕуBЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуAЃЌСЌНгOAЃЌЧв
ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуAЃЌСЌНгOAЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓІЄBOCЕФУцЛ§ЃЎ
ЃЈ2ЃЉЧѓЕуAЕФзјБъКЭЗДБШР§КЏЪ§![]() ЕФНтЮіЪНЃЎ
ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉЃЈ+10ЃЉ+ЃЈЉ4ЃЉ
ЃЈ2ЃЉЃЈЉ![]() ЃЉ+ЃЈЉ
ЃЉ+ЃЈЉ![]() ЃЉ+ЃЈЉ
ЃЉ+ЃЈЉ![]() ЃЉ+
ЃЉ+![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ5.6+ЃЈЉ0.9ЃЉ+4.4+ЃЈЉ8.1ЃЉ
ЃЈ4ЃЉЃЈЉ81ЃЉЁТ![]() ЁС
ЁС![]() ЁТЃЈЉ16ЃЉ
ЁТЃЈЉ16ЃЉ
ЃЈ5ЃЉЃЈЉ5ЃЉЁС49![]()
ЃЈ6ЃЉЃЈЉ125ЃЉЁС[2ЉЃЈЉ2ЃЉ]Љ300ЁТ6ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
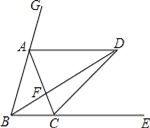
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЁЂCЗжБ№дкЁЯGBEЕФБпBGЁЂBEЩЯЃЌЧвAB=ACЃЌADЁЮBEЃЌЁЯGBEЕФЦНЗжЯпгыADНЛгкЕуDЃЌСЌНгCDЃЎ
ЧѓжЄЃКЂйAB=ADЃЛ
ЂкCDЦНЗжЁЯACEЃЎ
ЁОД№АИЁПЯъМћНтЮі.
ЁОНтЮіЁП(1)ЁпADЁЮBEЃЌ
ЁрЁЯADB=ЁЯDBCЃЌ
ЁпBDЦНЗжЁЯABCЃЌ
ЁрЁЯABD=ЁЯDBCЃЌ
ЁрЁЯABD=ЁЯADBЃЌ
ЁрAB=ADЃЛ
ЃЈ2ЃЉЁпADЁЮBEЃЌ
ЁрЁЯADC=ЁЯDCEЃЌ
гЩЂйжЊAB=ADЃЌ
гжЁпAB=ACЃЌ
ЁрAC=ADЃЌ
ЁрЁЯACD=ЁЯADCЃЌ
ЁрЁЯACD=ЁЯDCEЃЌ
ЁрCDЦНЗжЁЯACEЃЛ
ЕуОІЃКНЧЦНЗжЯпЮЪЬтЕФИЈжњЯпЬэМгМАЦфНтЬтФЃаЭ.
ЂйДЙСНБпЃКШчЭМЃЈ1ЃЉЃЌвбжЊ![]() ЦНЗж
ЦНЗж![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌ
ЃЌ ![]() ЃЌдђ
ЃЌдђ![]() .
.
ЂкНиСНБпЃКШчЭМЃЈ2ЃЉЃЌвбжЊ![]() ЦНЗж
ЦНЗж![]() ЃЌЕу
ЃЌЕу![]()
![]() ЩЯЃЌдк
ЩЯЃЌдк![]() ЩЯНиШЁ
ЩЯНиШЁ![]() ЃЌдђ
ЃЌдђ![]() Ёе
Ёе![]() .
.
ЂлНЧЦНЗжЯп+ЦНааЯпЁњЕШбќШ§НЧаЮЃК
ШчЭМЃЈ3ЃЉЃЌвбжЊ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ШчЭМЃЈ4ЃЉЃЌвбжЊ![]() ЦНЗж
ЦНЗж![]()
![]() ЃЌдђ
ЃЌдђ![]() .
.
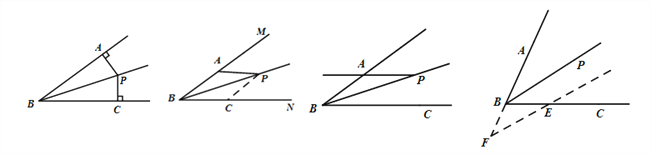
(1) (2) (3) (4)
ЂмШ§ЯпКЯвЛЃЈРћгУНЧЦНЗжЯп+ДЙЯпЁњЕШбќШ§НЧаЮЃЉЃК
ШчЭМЃЈ5ЃЉЃЌвбжЊ![]() ЦНЗж
ЦНЗж![]() ЃЌЧв
ЃЌЧв![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ ![]() .
.
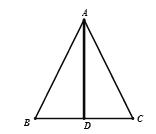
(5)
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
26
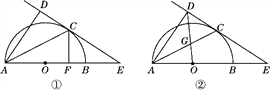
ЁОЬтФПЁПШчЭМЂйЃЌABЮЊАыдВЕФжБОЖЃЌOЮЊдВаФЃЌCЮЊдВЛЁЩЯвЛЕуЃЌADДЙжБгкЙ§CЕуЕФЧаЯпЃЌДЙзуЮЊDЃЌABЕФбгГЄЯпНЛжБЯпCDгкЕуE.
(1)ЧѓжЄЃКACЦНЗжЁЯDABЃЛ
(2)ШєABЃН4ЃЌBЮЊOEЕФжаЕуЃЌCFЁЭABЃЌДЙзуЮЊЕуFЃЌЧѓCFЕФГЄЃЛ
(3)ШчЭМЂкЃЌСЌНгODНЛACгкЕуGЃЌШє![]() ЃЌЧѓsinEЕФжЕЃЎ
ЃЌЧѓsinEЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
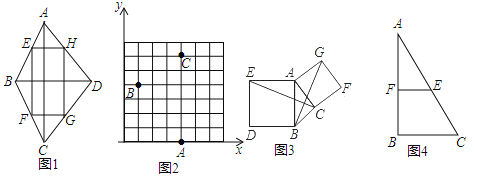
ЁОЬтФПЁПШчЭМ1ЃЌШєЫГДЮСЌНгЫФБпаЮABCDИїБпжаЕуЕУЕФЫФБпаЮEFGHЪЧОиаЮЃЌдђГЦдЫФБпаЮABCDЮЊЁАжаФИОиаЮЁБМДШєЫФБпаЮЕФЖдНЧЯпЛЅЯрДЙжБЃЌФЧУДетИіЫФБпаЮГЦЮЊЁАжаФИОиаЮЁБ.
ЃЈ1ЃЉШчЭМ2ЃЌдкжБНЧзјБъЯЕxOyжаЃЌвбжЊAЃЈ4ЃЌ0ЃЉЃЌBЃЈ1ЃЌ4ЃЉЃЌCЃЈ4ЃЌ6ЃЉЃЌЧыдкИёЕуЩЯБъГіDЕуЕФЮЛжУЃЈжЛБъвЛЕуМДПЩЃЉЃЌЪЙЫФБпаЮABCDЪЧжаФИОиаЮ.ВЂаДГіЕуDЕФзјБъ.
ЃЈ2ЃЉШчЭМ3ЃЌвдЁїABCЕФБпABЃЌACЮЊБпЃЌЯђШ§НЧаЮЭтзїе§ЗНаЮABDEМАACFGЃЌСЌНгCEЃЌBGЯрНЛгкЕуOЃЌЪдХаЖЯЫФБпаЮBEGCЪЧжаФИОиаЮЃПЫЕУїРэгЩ.
ЃЈ3ЃЉШчЭМ4ЃЌдкRtЁїABCжаЃЌABЃН8ЃЌBCЃН6ЃЌEЪЧаББпACЕФжаЕуЃЌFЪЧжБНЧБпABЕФжаЕуЃЌPЪЧжБНЧБпBCЩЯвЛЖЏЕуЃЌЪдЬНОПЃКЕБPCЃН_____ЪБЃЌЫФБпаЮBPEFЪЧжаФИОиаЮЃПЃЈжБНЧШ§НЧаЮжаЃЌ30ЁуНЧЫљЖдЕФжБНЧБпЪЧаББпЕФвЛАыЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуOЮЊЪ§жсЕФдЕуЃЌЕуAЁЂBдкЪ§жсЩЯЕФЮЛжУШчЭМЫљЪОЃЌЕуAБэЪОЕФЪ§ЮЊ5ЃЌЯпЖЮABЕФГЄЮЊЯпЖЮOAГЄЕФ1.2БЖ.ЕуCдкЪ§жсЩЯЃЌMЮЊЯпЖЮOCЕФжаЕу

ЃЈ1ЃЉЕуBБэЪОЕФЪ§ЮЊ____________
ЃЈ2ЃЉШєЯпЖЮBMЕФГЄЮЊ4.5ЃЌдђЯпЖЮACЕФГЄЮЊ___________
ЃЈ3ЃЉШєЯпЖЮACЕФГЄЮЊxЃЌЧѓЯпЖЮBMЕФГЄЃЈгУКЌxЕФЪНзгБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com