
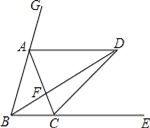
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.
【答案】详见解析.
【解析】(1)∵AD∥BE,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
(2)∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
点睛:角平分线问题的辅助线添加及其解题模型.
①垂两边:如图(1),已知![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() ,
, ![]() ,则
,则![]() .
.
②截两边:如图(2),已知![]() 平分
平分![]() ,点
,点![]()
![]() 上,在
上,在![]() 上截取
上截取![]() ,则
,则![]() ≌
≌![]() .
.
③角平分线+平行线→等腰三角形:
如图(3),已知![]() 平分
平分![]() ,
, ![]() ,则
,则![]() ;
;
如图(4),已知![]() 平分
平分![]()
![]() ,则
,则![]() .
.
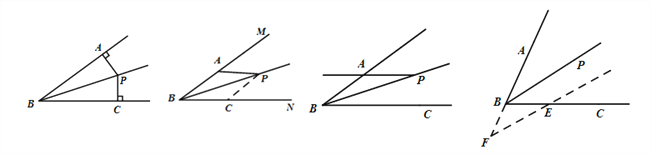
(1) (2) (3) (4)
④三线合一(利用角平分线+垂线→等腰三角形):
如图(5),已知![]() 平分
平分![]() ,且
,且![]() ,则
,则![]() ,
, ![]() .
.
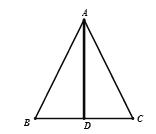
(5)
【题型】解答题
【结束】
26
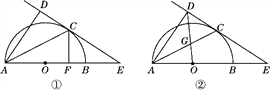
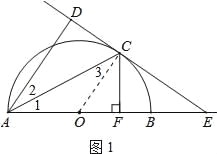
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
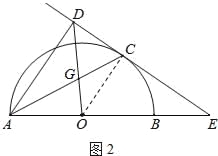
(3)如图②,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.
【答案】(1)证明见解析;(2)CF=![]() ;(3) sinE=
;(3) sinE=![]() .
.
【解析】试题分析:(1)连结OC,如图1,根据切线的性质得OC⊥DE,而AD⊥DE,根据平行线的性质得OC∥AD,所以∠2=∠3,加上∠1=∠3,则∠1=∠2,所以AC平分∠DAB;
(2)如图1,由B为OE的中点,AB为直径得到OB=BE=2,OC=2,在Rt△OCE中,由于OE=2OC,根据含30度的直角三角形三边的关系得∠OEC=30°,则∠COE=60°,由CF⊥AB得∠OFC=90°,所以∠OCF=30°,再根据含30度的直角三角形三边的关系得OF=![]() OC=1,CF=
OC=1,CF=![]() OF=
OF=![]() ;
;
(3)连结OC,如图2,先证明△OCG∽△DAG,利用相似的性质得![]() =
=![]() =
=![]() ,再证明△ECO∽△EDA,利用相似比得到
,再证明△ECO∽△EDA,利用相似比得到![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,代入求得OE=3R;最后在Rt△OCE中,根据正弦的定义求解.
,设⊙O的半径为R,OE=x,代入求得OE=3R;最后在Rt△OCE中,根据正弦的定义求解.
试题解析:(1)连结OC,如图1,∵DE与⊙O切于点C,∴OC⊥DE,
∵AD⊥DE,∴OC∥AD,∴∠2=∠3,∵OA=OC,∴∠1=∠3,
∴∠1=∠2,
即AC平分∠DAB;
(2)如图1,
∵直径AB=4,B为OE的中点,
∴OB=BE=2,OC=2,
在Rt△OCE中,OE=2OC,
∴∠OEC=30°,
∴∠COE=60°,∵CF⊥AB,∴∠OFC=90°,∴∠OCF=30°,∴OF=![]() OC=1,CF=
OC=1,CF=![]() OF=
OF=![]() ;
;
(3)连结OC,如图2,∵OC∥AD,∴△OCG∽△DAG,∴![]() =
=![]() =
=![]() ,∵OC∥AD,
,∵OC∥AD,
∴△ECO∽△EDA,∴![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,∴
,设⊙O的半径为R,OE=x,∴![]() =
=![]() ,解得OE=3R,
,解得OE=3R,
在Rt△OCE中,sin∠E=![]() =
=![]() =
=![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】已知:菱形ABCD中,∠B=60°,将含60°角的直角三角板的60°角的顶点放到菱形ABCD的顶点A处,两边分别与菱形的边BC,CD交于点F,E.
(1)(如图1)求证:AE=AF;
(2)连结EF,交AC于点H(如图2),试探究AB,AF,AH之间的关系;
(3)若AB=6,EF=2![]() ,且CE<DE,求FH的长.
,且CE<DE,求FH的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实根,且其中一个根为另一根的2倍,则称这样的方程为“倍根方”,以下关于倍根方程的说法正确的是______(填正确序号)
①方程x2﹣x﹣2=0是倍根方程.
②若(x﹣2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0.
③若点(p,q)在反比例函数y=![]() 的图象上,则关于x的方程px2+3x+q=0是倍根方程.
的图象上,则关于x的方程px2+3x+q=0是倍根方程.
④若方程ax2+bx+c=0是倍根方程且相异两点M(1+t,s)、N(4﹣t,s)都在抛物线y=ax2+bx+c上,则方程ax2+bx+c=0必有一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交x轴于点B(2,0),交y轴于点A(0,2),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=3,连接DA,∠DAC=90°.
(1)求直线AB的解析式.
(2)求D点坐标及过O、D、B三点的抛物线解析式.
(3)若点P是线段OB上的动点,过点P作x轴的垂线交AB于F,交(2)中抛物线于E,连CE,是否存在P使△BPF与△FCE相似?若存在,请求出P点坐标;若不存在说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
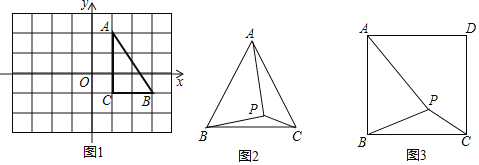
【题目】(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B= ;
(2)如图2,在等边三角形ABC内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和等边三角形ABC的边长;
,求∠BPC的度数和等边三角形ABC的边长;
(3)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和正方形ABCD的边长.
,求∠BPC的度数和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花园内有一块边长为a的正方形土地,园艺师设计了四种不同的图案,如下图的A、B、C、D所示,其中的阴影部分用于种植花草.种植花草部分面积最大的图案是( )(说明:A、B、C中圆弧的半径均为![]() ,D中圆弧的半径为a)
,D中圆弧的半径为a)
A. B.
B.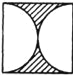 C.
C.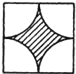 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
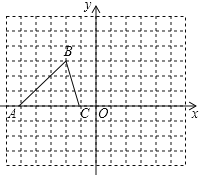
【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
(1)画出△ABC关于坐标原点O成中心对称的△![]() ;
;
(2)将△ABC绕坐标原点O顺时针旋转90°,画出对应的△![]() ,
,
(3)若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,请直接写出在第四象限中的
为顶点的四边形为平行四边形,请直接写出在第四象限中的![]() 坐标____.
坐标____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b是表示两个不同点A,B的有理数,且|a|=5,|b|=2,它们在数轴的位置如图所示.
![]()
(1)试确定a,b的值;并求表示a,b两数的点的距离;
(2)若点C在数轴上,点C到点A的距离是点C到点B距离的3倍,则点C表示的数为_ ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com