
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实根,且其中一个根为另一根的2倍,则称这样的方程为“倍根方”,以下关于倍根方程的说法正确的是______(填正确序号)
①方程x2﹣x﹣2=0是倍根方程.
②若(x﹣2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0.
③若点(p,q)在反比例函数y=![]() 的图象上,则关于x的方程px2+3x+q=0是倍根方程.
的图象上,则关于x的方程px2+3x+q=0是倍根方程.
④若方程ax2+bx+c=0是倍根方程且相异两点M(1+t,s)、N(4﹣t,s)都在抛物线y=ax2+bx+c上,则方程ax2+bx+c=0必有一个根为![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】仔细填一填:
把下列各数填入相应的大括号里:
5,-1,0,-6,+8,0.3,-![]() ,+
,+![]() ,-0.72,…
,-0.72,…
① 正数集合:{ __________________ …}
② 整数集合:{__________________…}
③ 负数集合:{ __________________ …}
④ 分数集合:{__________________ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC中,![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
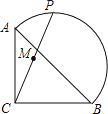
A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
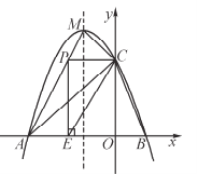
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD面积等于6时,求点D的坐标;
(3)点P在线段AM上,当PC与y轴垂直时,过点P作![]() 轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
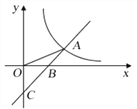
【题目】如图,直线![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点B,与反比例函数
轴交于点B,与反比例函数![]() 的图象在第一象限交于点A,连接OA,且
的图象在第一象限交于点A,连接OA,且![]() .
.
(1)求ΔBOC的面积.
(2)求点A的坐标和反比例函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
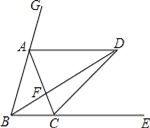
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.
【答案】详见解析.
【解析】(1)∵AD∥BE,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
(2)∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
点睛:角平分线问题的辅助线添加及其解题模型.
①垂两边:如图(1),已知![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() ,
, ![]() ,则
,则![]() .
.
②截两边:如图(2),已知![]() 平分
平分![]() ,点
,点![]()
![]() 上,在
上,在![]() 上截取
上截取![]() ,则
,则![]() ≌
≌![]() .
.
③角平分线+平行线→等腰三角形:
如图(3),已知![]() 平分
平分![]() ,
, ![]() ,则
,则![]() ;
;
如图(4),已知![]() 平分
平分![]()
![]() ,则
,则![]() .
.
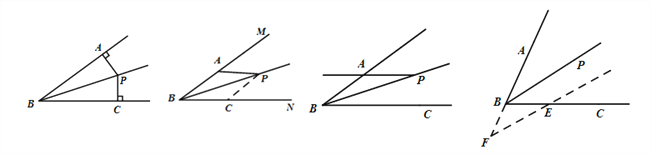
(1) (2) (3) (4)
④三线合一(利用角平分线+垂线→等腰三角形):
如图(5),已知![]() 平分
平分![]() ,且
,且![]() ,则
,则![]() ,
, ![]() .
.
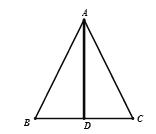
(5)
【题型】解答题
【结束】
26
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.
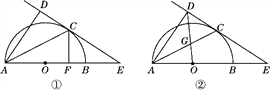
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有![]() 、
、![]() 、
、![]() 三地,甲、乙两车同时从
三地,甲、乙两车同时从![]() 地出发,分别匀速前往
地出发,分别匀速前往![]() 地、
地、![]() 地,甲车到达
地,甲车到达![]() 地停留一段时间后原速原路返回,乙车到达
地停留一段时间后原速原路返回,乙车到达![]() 地后立即原速原路返回,乙车比甲车早1小时返回到
地后立即原速原路返回,乙车比甲车早1小时返回到![]() 地,甲、乙两车各自行驶的路程
地,甲、乙两车各自行驶的路程![]() (千米)与时间
(千米)与时间![]() (小时)(从两车出发时开始计时)之间的函数图像如图所示.
(小时)(从两车出发时开始计时)之间的函数图像如图所示.
(1)甲车到达![]() 地停留的时间为 小时;
地停留的时间为 小时;
(2)求甲车返回![]() 地的图中
地的图中![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)直接写出两车在图中相遇时![]() 的值.
的值.
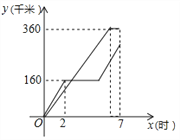
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com