
【题目】在一条公路上顺次有![]() 、
、![]() 、
、![]() 三地,甲、乙两车同时从
三地,甲、乙两车同时从![]() 地出发,分别匀速前往
地出发,分别匀速前往![]() 地、
地、![]() 地,甲车到达
地,甲车到达![]() 地停留一段时间后原速原路返回,乙车到达
地停留一段时间后原速原路返回,乙车到达![]() 地后立即原速原路返回,乙车比甲车早1小时返回到
地后立即原速原路返回,乙车比甲车早1小时返回到![]() 地,甲、乙两车各自行驶的路程
地,甲、乙两车各自行驶的路程![]() (千米)与时间
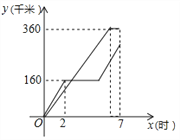
(千米)与时间![]() (小时)(从两车出发时开始计时)之间的函数图像如图所示.
(小时)(从两车出发时开始计时)之间的函数图像如图所示.
(1)甲车到达![]() 地停留的时间为 小时;
地停留的时间为 小时;
(2)求甲车返回![]() 地的图中
地的图中![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)直接写出两车在图中相遇时![]() 的值.
的值.
【答案】(1)3;(2)y=80x-240;(3)两车在途中相遇时x的值为![]() 或
或![]() .
.
【解析】试题分析:(1)根据甲的行进方式,观察图象,可知时间.(2)利用待定系数法求一次函数解析式.(3)分别求出甲乙速度,第一次第二次相遇分别计算.
试题解析:
(1)由图象知3小时.
(2)设y=kx+b,图象过(5,160),(7,320),
![]() ,解得
,解得![]() .
.
甲车返回A地图中y与x之间的关系是y=80x-240.
(3)由题意得,
甲车速是160![]() 千米/时.
千米/时.
乙车的车速是360![]() 千米/时.
千米/时.
第一次相遇时间是160![]() =
=![]() 小时.
小时.
第二次相遇时间是x,(360-60x)=160,(360-60x)=320-(80x-240),
解x=![]() ,x=10(舍去).
,x=10(舍去).
所以相遇时是![]() ,
, ![]() ,小时.
,小时.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实根,且其中一个根为另一根的2倍,则称这样的方程为“倍根方”,以下关于倍根方程的说法正确的是______(填正确序号)
①方程x2﹣x﹣2=0是倍根方程.
②若(x﹣2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0.
③若点(p,q)在反比例函数y=![]() 的图象上,则关于x的方程px2+3x+q=0是倍根方程.
的图象上,则关于x的方程px2+3x+q=0是倍根方程.
④若方程ax2+bx+c=0是倍根方程且相异两点M(1+t,s)、N(4﹣t,s)都在抛物线y=ax2+bx+c上,则方程ax2+bx+c=0必有一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
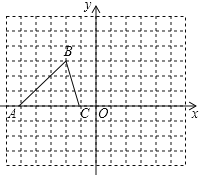
【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
(1)画出△ABC关于坐标原点O成中心对称的△![]() ;
;
(2)将△ABC绕坐标原点O顺时针旋转90°,画出对应的△![]() ,
,
(3)若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,请直接写出在第四象限中的
为顶点的四边形为平行四边形,请直接写出在第四象限中的![]() 坐标____.
坐标____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b是表示两个不同点A,B的有理数,且|a|=5,|b|=2,它们在数轴的位置如图所示.
![]()
(1)试确定a,b的值;并求表示a,b两数的点的距离;
(2)若点C在数轴上,点C到点A的距离是点C到点B距离的3倍,则点C表示的数为_ ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB边上的一点,∠A=36°,AC=BC,AC2=ADAB.

(1)求证:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值(精确到0.001).
查看答案和解析>>
科目:初中数学 来源: 题型:
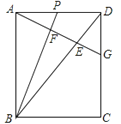
【题目】如图,在长方形![]() 中,
中, ![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)当![]() =
=![]() ,且
,且![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() =
=![]() .
.
(2)在(1)的条件下,求![]() 的值;
的值;
(3)类比探究:若![]() =3
=3![]() ,
, ![]() =2
=2![]() ,则
,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.
①求证:△ABC∽△DCA;②求证:△ABC是比例三角形;
(3)如图2,在(2)的条件下,当∠ADC=90°时,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
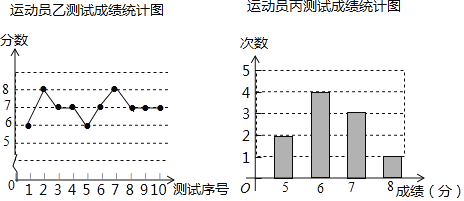
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com