
【题目】如图,在△ABC中,D为AB边上的一点,∠A=36°,AC=BC,AC2=ADAB.

(1)求证:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值(精确到0.001).
【答案】(1)见解析;(2)AC≈0.618.
【解析】
(1)由条件可证明△ACD∽△ABC,可得∠ACD=∠B=36°,可求得DC=DA,且∠CDB=∠DCB=72°,可得BC=BD,可证得结论;
(2)过C作AE⊥AB,利用等腰三角形的性质可知AE=![]() ,在Rt△ACE中利用∠A的余弦值可求得AC.
,在Rt△ACE中利用∠A的余弦值可求得AC.
(1)证明:∵AC2=ADAB,
∴![]() =
=![]() ,且∠CAD=∠BAC,
,且∠CAD=∠BAC,
∴△ACD∽△ABC,
∴∠ACD=∠B,
又∵AC=BC,
∴∠A=∠B=36°,
∴∠A=∠ACD=36°,
∴AD=CD,即△ADC为等腰三角形,
∴∠CDB=2∠A=72°,且∠B=36°,
∴∠BCD=∠CDB=72°,
∴BC=BD,
∴△BDC为等腰三角形;
(2)解:如图,过C作CE⊥AB于点E,
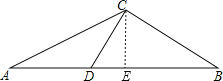
∵AC=BC,
∴AE=![]() AB=
AB=![]() ,
,
在Rt△ACE中,cos∠A=![]() ,
,
∴![]() =cos36°,
=cos36°,
∴AC=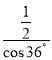 ≈
≈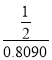 =0.618.
=0.618.
∴AC≈0.618.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数y=2x的图象与反比例函数y=![]() 的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )
的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )

A.(﹣8,0)B.(﹣6,0)C.(﹣![]() ,0)D.(﹣
,0)D.(﹣![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数3.3 ,-2 ,0 ,![]() ,-3.5 ;
,-3.5 ;
(1) 比较这些数的绝对值的大小,并将这些数的绝对值用“>”号连接起来;
(2) 比较这些数的相反数的大小,并将这些数的相反数用“<”号连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.
(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有![]() 、
、![]() 、
、![]() 三地,甲、乙两车同时从
三地,甲、乙两车同时从![]() 地出发,分别匀速前往
地出发,分别匀速前往![]() 地、
地、![]() 地,甲车到达
地,甲车到达![]() 地停留一段时间后原速原路返回,乙车到达
地停留一段时间后原速原路返回,乙车到达![]() 地后立即原速原路返回,乙车比甲车早1小时返回到
地后立即原速原路返回,乙车比甲车早1小时返回到![]() 地,甲、乙两车各自行驶的路程
地,甲、乙两车各自行驶的路程![]() (千米)与时间
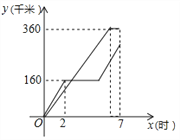
(千米)与时间![]() (小时)(从两车出发时开始计时)之间的函数图像如图所示.
(小时)(从两车出发时开始计时)之间的函数图像如图所示.
(1)甲车到达![]() 地停留的时间为 小时;
地停留的时间为 小时;
(2)求甲车返回![]() 地的图中
地的图中![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)直接写出两车在图中相遇时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,①求边CP的长;②求边AB的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=kx+b(k,b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),抛物线y=﹣x2+4x+1与y轴交于点C,点E在抛物线y=﹣x2+4x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )

A.2B.4C.2.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为< x >,即已知n为正整数,如果n-![]() ≤x<n+
≤x<n+![]() ,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=
,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=![]() 的非负实数x的值为____.
的非负实数x的值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com