
【题目】已知:如图,直线y=kx+b(k,b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),抛物线y=﹣x2+4x+1与y轴交于点C,点E在抛物线y=﹣x2+4x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )

A.2B.4C.2.5D.3
【答案】B
【解析】
设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,则可知当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,由C点坐标可确定出C′,F点的坐标,即可求得CE+EF的最小值.
解:如图,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,
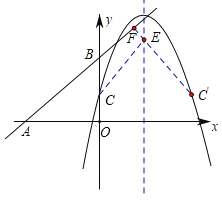
∴CE+EF=C′E+EF,
∴当F、E、C′三点共线且C′F⊥AB时CE+EF最小,
∵直线y=kx+b(k,b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),
∴![]() ,
,
解得![]() ,
,
∴直线解析式为y=![]() x+3;
x+3;
∵抛物线y=﹣x2+4x+1与y轴交于点C,
∴C(0,1),
∴C′(4,1),
∴可设直线C′F的解析式为y=﹣![]() x+
x+![]() ,
,
由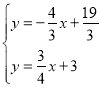 ,解得
,解得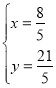 ,
,
∴F(![]() ,
,![]() ),
),
∴C′F= =4,
=4,
即CE+EF的最小值为4,
故选:B.


科目:初中数学 来源: 题型:
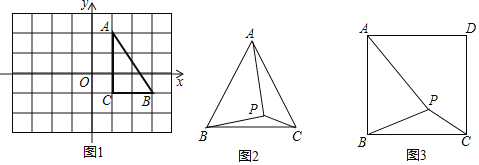
【题目】(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B= ;
(2)如图2,在等边三角形ABC内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和等边三角形ABC的边长;
,求∠BPC的度数和等边三角形ABC的边长;
(3)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和正方形ABCD的边长.
,求∠BPC的度数和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB边上的一点,∠A=36°,AC=BC,AC2=ADAB.

(1)求证:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值(精确到0.001).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.
①求证:△ABC∽△DCA;②求证:△ABC是比例三角形;
(3)如图2,在(2)的条件下,当∠ADC=90°时,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学用两个完全相同的直角三角形纸片重叠在一起(如图1)固定△ABC不动,将△DEF沿线段AB向右平移.
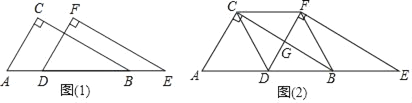
(1)若∠A=60°,斜边AB=4,设AD=x(0≤x≤4),两个直角三角形纸片重叠部分的面积为y,试求出y与x的函数关系式;
(2)在运动过程中,四边形CDBF能否为正方形,若能,请指出此时点D的位置,并说明理由;若不能,请你添加一个条件,并说明四边形CDBF为正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的七边形ABCDEFG中,∠1、∠2、∠3、∠4 四个角的外角和为180°,∠5 的外角为60°,BP、DP 分别平分∠ABC、∠CDE,则∠BPD 的度数是( )

A. 130° B. 120° C. 110° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,![]() 点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒
点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.
个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.
(1)用含t的代数式表示线段AQ的长.
(2)当点P在线段AB上运动时,求PQ与△ABC一边垂直时t的值.
(3)设△APQ的面积为S(S>0),求S与t的函数关系式.
(4)当△APQ是以PQ为腰的等腰三角形时,直接写出t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com