
����Ŀ��ijͬѧ��������ȫ��ͬ��ֱ��������ֽƬ�ص���һ����ͼ1���̶���ABC����������DEF���߶�AB����ƽ�ƣ�
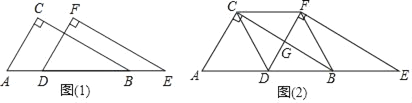
��1������A=60����б��AB=4����AD=x��0��x��4��������ֱ��������ֽƬ�ص����ֵ����Ϊy�������y��x�ĺ�����ϵʽ��
��2�����˶������У��ı���CDBF�ܷ�Ϊ�����Σ����ܣ���ָ����ʱ��D��λ�ã���˵�����ɣ������ܣ���������һ����������˵���ı���CDBFΪ�����Σ�
���𰸡���1��y=![]() ��0��x��4����(2) ����Ϊ�����Σ�����������AC=BCʱ������D�˶���AB�е�λ��ʱ�ı���CDBFΪ�����Σ�
��0��x��4����(2) ����Ϊ�����Σ�����������AC=BCʱ������D�˶���AB�е�λ��ʱ�ı���CDBFΪ�����Σ�
����������������1������ƽ�Ƶ����ʵõ�DF��AC��������ƽ���ߵ����ʡ����ɶ������GD=![]() ��BG=
��BG=![]() =
=![]() �������������ε������ʽ�г�������ϵʽ����2������Ϊ������,��������:AC=BCʱ,��D�˶���AB�е�ʱ���ı���CDBFΪ�����Σ���D�˶���AB�е�ʱ���ı���CDBF�����Σ�������ֱ��������б���ϵ����ߵ���б�ߵ�һ������֪CD=
�������������ε������ʽ�г�������ϵʽ����2������Ϊ������,��������:AC=BCʱ,��D�˶���AB�е�ʱ���ı���CDBFΪ�����Σ���D�˶���AB�е�ʱ���ı���CDBF�����Σ�������ֱ��������б���ϵ����ߵ���б�ߵ�һ������֪CD=![]() AB,BF=
AB,BF=![]() DE,����AD=CD=BD=CF,����BE=AD,��CD=BD=BF=CF,���ı���CDBF�����Σ�������һ�ڽ�Ϊֱ�ǵ�����������������������.
DE,����AD=CD=BD=CF,����BE=AD,��CD=BD=BF=CF,���ı���CDBF�����Σ�������һ�ڽ�Ϊֱ�ǵ�����������������������.
�������1����ͼ��1��
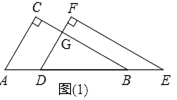
��DF��AC��
���DGB=��C=90�㣬��GDB=��A=60�㣬��GBD=30��
��BD=4��x��
��GD=![]() ��BG=
��BG=![]() =
=![]()
y=S��BDG=![]() ��
��![]() ��
��![]() =
=![]() ��0��x��4����
��0��x��4����
��2������Ϊ�����Σ�����������AC=BCʱ������D�˶���AB�е�λ��ʱ�ı���CDBFΪ�����Σ�
�ߡ�ACB=��DFE=90�㣬D��AB���е�
��CD=![]() AB��BF=
AB��BF=![]() DE��
DE��
��CD=BD=BF=BE��
��CF=BD��
��CD=BD=BF=CF��
���ı���CDBF�����Σ�
��AC=BC��D��AB���е㣮
��CD��AB����CDB=90��
���ı���CDBFΪ���Σ�
���ı���CDBF�������Σ�


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��һ�κ���y��2x��ͼ���뷴��������y��![]() ��ͼ���ڵ�һ�����ڵĽ��㣬AB��x���ڵ�B����C��x��ĸ������ϣ��ҡ�ACB����OAB����OAB�����Ϊ4�����C������Ϊ��������
��ͼ���ڵ�һ�����ڵĽ��㣬AB��x���ڵ�B����C��x��ĸ������ϣ��ҡ�ACB����OAB����OAB�����Ϊ4�����C������Ϊ��������

A.����8��0��B.����6��0��C.����![]() ��0��D.����
��0��D.����![]() ��0��
��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD��һ����AD��8��������ABCD�۵���ʹ�ö���B����CD���ϵ�P�㴦��

��1����֤����OCP�ס�PDA��
��2������OCP���PDA�������Ϊ1��4�������CP�ij��������AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ֱ��y��kx+b��k��bΪ�������ֱ���x�ᡢy�ύ�ڵ�A����4��0����B��0��3����������y����x2+4x+1��y�ύ�ڵ�C����E��������y����x2+4x+1�ĶԳ������ƶ�����F��ֱ��AB���ƶ���CE+EF����Сֵ�ǣ�������

A.2B.4C.2.5D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������1��2��3��4��2016���г���ͼ��ʾ����ʽ.

��1����һ�����������ס4��������������С������Ϊ![]() ,���������ú�
,���������ú�![]() ʽ�ӱ�ʾ������������ס��4����֮�͵���418ʱ��
ʽ�ӱ�ʾ������������ס��4����֮�͵���418ʱ��![]() ֵ�Ƕ��٣�
ֵ�Ƕ��٣�
��2������ס��4����֮���ܷ����724������ܣ��������ʱxֵ��������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȵ��������ȿɱ�ʾΪ1��a+b��a����ʽ���ֿɱ�ʾΪ0��![]() ��b����ʽ����12a2��5ab��_____��
��b����ʽ����12a2��5ab��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() .
.
(1)��֪![]() ����
����![]() �Ķ���;
�Ķ���;
(2)���![]() ��
��![]() ��ƽ���ߣ���ô
��ƽ���ߣ���ô![]() ��
��![]() ��ƽ������?˵������.
��ƽ������?˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ԷǸ�ʵ��x����������������λ��ֵ��Ϊ< x >������֪nΪ�����������n��![]() ��x��n��
��x��n��![]() ����ô< x >��n�����磺< 0 >��< 0.48 >��0��< 0.64 >��< 1.493 >��1��< 2 >��2��< 3.5 >��< 4.12 >��4���������㷽��< x >��
����ô< x >��n�����磺< 0 >��< 0.48 >��0��< 0.64 >��< 1.493 >��1��< 2 >��2��< 3.5 >��< 4.12 >��4���������㷽��< x >��![]() �ķǸ�ʵ��x��ֵΪ____.
�ķǸ�ʵ��x��ֵΪ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ������ֱ���A��B��C���㣬��֪��A��һ3��O����B(1��0)����P�ڵڶ������ڵ����������˶�����PD��
������ֱ���A��B��C���㣬��֪��A��һ3��O����B(1��0)����P�ڵڶ������ڵ����������˶�����PD��![]() ���ӵ�D����ֱ��AC�ڵ�E��
���ӵ�D����ֱ��AC�ڵ�E��

(1) ![]()
(2)����P��PF��AC�ڵ�F����PEF���ܳ�ȡ���ֵʱ��P�����꣮
(3)����AP������APΪ��������ֱ�ǡ�APQ��������Qǡ�����������ߵĶԳ�����ʱ�����Ӧ��P������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com