
【题目】如图,抛物线![]() 与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上
与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上![]() 轴子点D,交直线AC于点E.
轴子点D,交直线AC于点E.

(1) ![]()
(2)过点P作PF⊥AC于点F.求当△PEF的周长取最大值时点P的坐标.
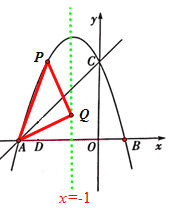
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求对应的P点坐标.
【答案】(1) -2; 3 ;(2)( ![]() ,
, ![]() )(3)
)(3) 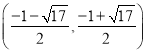 ,
, ![]()
【解析】试题分析:(1)将A、B两点坐标代入解析式中即可求出b、c的值;
(2)通过点P、E的坐标可求出PE=![]() ,由题可知,△PEF为等腰直角三角形,当PE最大时,此三角形的周长最大,求出令PE最大的x值,即可求出P点的坐标;
,由题可知,△PEF为等腰直角三角形,当PE最大时,此三角形的周长最大,求出令PE最大的x值,即可求出P点的坐标;
(3)对以P、Q、A三个顶点的角分别为直角时所形成的等腰直角三角形进行分类讨论即可.
解:(1)∵A(一3,O),B(1,0)在抛物线![]() 的图象上,
的图象上,
∴![]()
解得![]()
故答案为:-2,3 ;
(2)∵C(0,3),A(-3,0)
∴AO=CO
∴∠CAO=45°
∵PD上![]() 轴于点D
轴于点D
∴∠ADE=90°
∴∠AED=45°
∵PF⊥AC于点F
且∠PEF=∠AED=45°
∴△PEF为等腰直角三角形
∴当PE最大时,此三角形的周长最大,
由C(0,3),A(-3,0)可知直线AC的解析式为
![]()
设P(x, ![]() ),则E点坐标为(x,x+3)
),则E点坐标为(x,x+3)
∴PE=![]() (-3<x<0)
(-3<x<0)
∵当![]() 时,PE最大,即此时△PEF的周长取最大值
时,PE最大,即此时△PEF的周长取最大值
∴P点坐标为(![]() ,
,![]() )
)
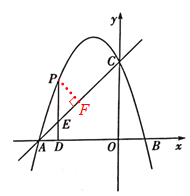
(3)有三种情况:
①当∠APQ=90°且PA=PQ时,P点坐标为
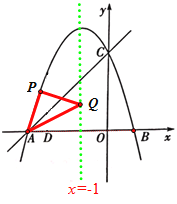
②当∠PAQ=90°且AP=AQ时,P点坐标为![]()
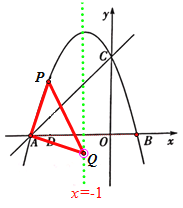
③当∠AQP=90°且PQ=AQ时,P点坐标为![]()
故P点坐标为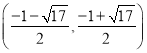 ,
, ![]()


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,则此正方形落在x轴正半轴的顶点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.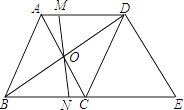
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )

A. 6![]() B. -6
B. -6![]() C. 12
C. 12![]() D. -12
D. -12![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com