
【题目】在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,则此正方形落在x轴正半轴的顶点坐标为 .
【答案】(1.5,0)或(1,0)
【解析】解:分两种情况;
①如图1, 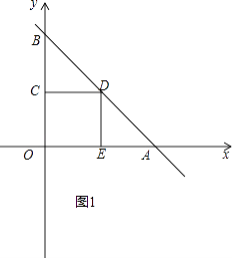
令x=0,则y=3,令y=0,则x=3,
∴OA=OB=3,
∴∠BAO=45°,
∵DE⊥OA,
∴DE=AE,
∵四边形COED是正方形,
∴OE=DE,
∴OE=AE,
∴OE= ![]() OA=1.5,
OA=1.5,
∴E(1.5,0);
②如图2, 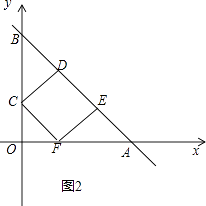
由①知△OFC,△EFA是等腰直角三角形,
∴CF= ![]() OF,AF=
OF,AF= ![]() EF,
EF,
∵四边形CDEF是正方形,
∴EF=CF,
∴AF= ![]() ×
× ![]() OF=2OF,
OF=2OF,
∴OA=OF+2OF=3,
∴OF=1,
∴F(1,0).
故答案为(1.5,0)或(1,0).
讨论①根据正方形的性质由四边形COED是正方形,得到四边相等,求出E点的坐标;②由①知△OFC,△EFA是等腰直角三角形,根据正方形的性质和勾股定理,求出AF、OA、OF的值,求出F点的坐标.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
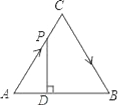
A.  B.
B.  C.
C. 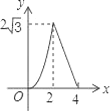 D.
D. 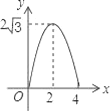
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分):10、12、15、10、16、18、19、18、20、18、18、20、28、22、30、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( )
A.4组
B.5组
C.6组
D.7组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】统计显示,2013年底某市各类高中在校学生人数约是11.4万人,将11.4万用科学记数法表示应为( )
A.11.4×104
B.1.14×104
C.1.14×105
D.0.114×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣6x+9=1的两个解恰好分别是等腰△ABC的底边长和腰长,则△ABC的周长为( )
A. 10 B. 10或8 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣6x2可以看作是由抛物线y=﹣6x2+5按下列何种变换得到( )
A.向上平移5个单位
B.向下平移5个单位
C.向左平移5个单位
D.向右平移5个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上
与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上![]() 轴子点D,交直线AC于点E.
轴子点D,交直线AC于点E.

(1) ![]()
(2)过点P作PF⊥AC于点F.求当△PEF的周长取最大值时点P的坐标.
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求对应的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t.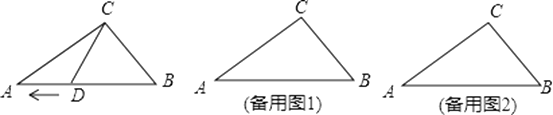
(1)AB= cm,AB边上的高为 cm;
(2)点D在运动过程中,当△BCD为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有40个数据,共分成6组,第1~4组的频数分别为10,5,7,6,第5组的频率是0.1,则第6组的频数是( )
A.8
B.28
C.32
D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com