
ЁОЬтФПЁПШєвЛИіШ§НЧаЮвЛЬѕБпЕФЦНЗНЕШгкСэСНЬѕБпЕФГЫЛ§ЃЌЮвУЧАбетИіШ§НЧаЮНазіБШР§Ш§НЧаЮЃЎ

ЃЈ1ЃЉвбжЊЁїABCЪЧБШР§Ш§НЧаЮЃЌABЃН2ЃЌBCЃН3ЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФACЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЖдНЧЯпBDЦНЗжЁЯABCЃЌЁЯBACЃНЁЯADCЃЎ
ЂйЧѓжЄЃКЁїABCЁзЁїDCAЃЛЂкЧѓжЄЃКЁїABCЪЧБШР§Ш§НЧаЮЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЁЯADCЃН90ЁуЪБЃЌЧѓГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉACЃН![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЛЃЈ2ЃЉЂйМћНтЮіЃЛЂкМћНтЮіЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉЂйМћНтЮіЃЛЂкМћНтЮіЃЛЃЈ3ЃЉ![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнБШР§Ш§НЧаЮЕФЖЈвхЗжAB2ЃНBCACЁЂBC2ЃНABACЁЂAC2ЃНABBCШ§жжЧщПіЗжБ№ДњШыМЦЫуПЩЕУЃЛ
ЃЈ2ЃЉЂйЯШХаЖЯГіЁЯACBЃНЁЯCADЃЌЕУГіЁїABCЁзЁїDCAЃЛ
ЂкгЩЁїABCЁзЁїDCAЕУГіCA2ЃНBCADЃЌдйгЩЁЯADBЃНЁЯCBDЃНЁЯABDжЊABЃНADМДПЩЕУЃЛ
ЃЈ3ЃЉзїAHЁЭBDЃЌгЩABЃНADжЊЃЌBHЃН![]() BDЃЌдйжЄЁїABHЁзЁїDBCЕУABBCЃНBHDBЃЌМДABBCЃН
BDЃЌдйжЄЁїABHЁзЁїDBCЕУABBCЃНBHDBЃЌМДABBCЃН![]() BD2ЃЌНсКЯABBCЃНAC2ЭЦГі
BD2ЃЌНсКЯABBCЃНAC2ЭЦГі![]() BD2ЃНAC2ЃЌОнДЫПЩЕУД№АИЃЎ
BD2ЃНAC2ЃЌОнДЫПЩЕУД№АИЃЎ
НтЃКЃЈ1ЃЉЁпЁїABCЪЧБШР§Ш§НЧаЮЃЌЧвABЃН2ЁЂBCЃН3ЃЌ
ЂйЕБAB2ЃНBCACЪБЃЌЕУЃК4ЃН3ACЃЌНтЕУЃКACЃН![]() ЃЛ
ЃЛ
ЂкЕБBC2ЃНABACЪБЃЌЕУЃК9ЃН2ACЃЌНтЕУЃКACЃН![]() ЃЛ
ЃЛ
ЂлЕБAC2ЃНABBCЪБЃЌЕУЃКAC2ЃН6ЃЌНтЕУЃКACЃН![]() ЃЈИКжЕЩсШЅЃЉЃЛ
ЃЈИКжЕЩсШЅЃЉЃЛ
ЫљвдЕБACЃН![]() Лђ
Лђ![]() Лђ
Лђ![]() ЪБЃЌЁїABCЪЧБШР§Ш§НЧаЮЃЛ
ЪБЃЌЁїABCЪЧБШР§Ш§НЧаЮЃЛ
ЃЈ2ЃЉЂйЁпADЁЮBCЃЌ
ЁрЁЯACBЃНЁЯCADЃЌ
гжЁпЁЯBACЃНЁЯADCЃЌ
ЁрЁїABCЁзЁїDCAЃЌ
ЂкгЩЂйжЊЃЌЁїABCЁзЁїDCAЃЌ
Ёр![]() ЃЌМДCA2ЃНBCADЃЌ
ЃЌМДCA2ЃНBCADЃЌ
ЁпADЁЮBCЃЌ
ЁрЁЯADBЃНЁЯCBDЃЌ
ЁпBDЦНЗжЁЯABCЃЌ
ЁрЁЯABDЃНЁЯCBDЃЌ
ЁрЁЯADBЃНЁЯABDЃЌ
ЁрABЃНADЃЌ
ЁрCA2ЃНBCABЃЌ
ЁрЁїABCЪЧБШР§Ш§НЧаЮЃЛ
ЃЈ3ЃЉШчЭМЃЌЙ§ЕуAзїAHЁЭBDгкЕуHЃЌ

ЁпABЃНADЃЌ
ЁрBHЃН![]() BDЃЌ
BDЃЌ
ЁпADЁЮBCЃЌЁЯADCЃН90ЁуЃЌ
ЁрЁЯBCDЃН90ЁуЃЌ
ЁрЁЯBHAЃНЁЯBCDЃН90ЁуЃЌ
гжЁпЁЯABHЃНЁЯDBCЃЌ
ЁрЁїABHЁзЁїDBCЃЌ
Ёр![]() ЃЌМДABBCЃНBHDBЃЌ
ЃЌМДABBCЃНBHDBЃЌ
ЁрABBCЃН![]() BD2ЃЌ
BD2ЃЌ
гжЁпABBCЃНAC2ЃЌ
Ёр![]() BD2ЃНAC2ЃЌ
BD2ЃНAC2ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЎ
ЃЎ


 аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИ
аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
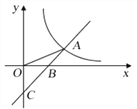
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсНЛгкЕуCЃЌгы
жсНЛгкЕуCЃЌгы![]() жсНЛгкЕуBЃЌгыЗДБШР§КЏЪ§
жсНЛгкЕуBЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуAЃЌСЌНгOAЃЌЧв
ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуAЃЌСЌНгOAЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓІЄBOCЕФУцЛ§ЃЎ
ЃЈ2ЃЉЧѓЕуAЕФзјБъКЭЗДБШР§КЏЪ§![]() ЕФНтЮіЪНЃЎ
ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§3.3 ЃЌЃ2 ЃЌ0 ЃЌ![]() ЃЌЃ3.5 ЃЛ
ЃЌЃ3.5 ЃЛ
(1) БШНЯетаЉЪ§ЕФОјЖджЕЕФДѓаЁЃЌВЂНЋетаЉЪ§ЕФОјЖджЕгУЁАЃОЁБКХСЌНгЦ№РДЃЛ
(2) БШНЯетаЉЪ§ЕФЯрЗДЪ§ЕФДѓаЁЃЌВЂНЋетаЉЪ§ЕФЯрЗДЪ§гУЁАЃМЁБКХСЌНгЦ№РДЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
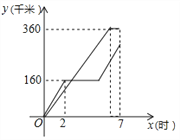
ЁОЬтФПЁПдквЛЬѕЙЋТЗЩЯЫГДЮга![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕиЃЌМзЁЂввСНГЕЭЌЪБДг
Ш§ЕиЃЌМзЁЂввСНГЕЭЌЪБДг![]() ЕиГіЗЂЃЌЗжБ№дШЫйЧАЭљ
ЕиГіЗЂЃЌЗжБ№дШЫйЧАЭљ![]() ЕиЁЂ
ЕиЁЂ![]() ЕиЃЌМзГЕЕНДя
ЕиЃЌМзГЕЕНДя![]() ЕиЭЃСєвЛЖЮЪБМфКѓдЫйдТЗЗЕЛиЃЌввГЕЕНДя
ЕиЭЃСєвЛЖЮЪБМфКѓдЫйдТЗЗЕЛиЃЌввГЕЕНДя![]() ЕиКѓСЂМДдЫйдТЗЗЕЛиЃЌввГЕБШМзГЕдч1аЁЪБЗЕЛиЕН
ЕиКѓСЂМДдЫйдТЗЗЕЛиЃЌввГЕБШМзГЕдч1аЁЪБЗЕЛиЕН![]() ЕиЃЌМзЁЂввСНГЕИїздааЪЛЕФТЗГЬ
ЕиЃЌМзЁЂввСНГЕИїздааЪЛЕФТЗГЬ![]() ЃЈЧЇУзЃЉгыЪБМф
ЃЈЧЇУзЃЉгыЪБМф![]() ЃЈаЁЪБЃЉЃЈДгСНГЕГіЗЂЪБПЊЪММЦЪБЃЉжЎМфЕФКЏЪ§ЭМЯёШчЭМЫљЪО.
ЃЈаЁЪБЃЉЃЈДгСНГЕГіЗЂЪБПЊЪММЦЪБЃЉжЎМфЕФКЏЪ§ЭМЯёШчЭМЫљЪО.
ЃЈ1ЃЉМзГЕЕНДя![]() ЕиЭЃСєЕФЪБМфЮЊ аЁЪБЃЛ
ЕиЭЃСєЕФЪБМфЮЊ аЁЪБЃЛ
ЃЈ2ЃЉЧѓМзГЕЗЕЛи![]() ЕиЕФЭМжа
ЕиЕФЭМжа![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉжБНгаДГіСНГЕдкЭМжаЯргіЪБ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊОиаЮABCDЕФвЛЬѕБпADЃН8ЃЌНЋОиаЮABCDелЕўЃЌЪЙЕУЖЅЕуBТфдкCDБпЩЯЕФPЕуДІЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїOCPЁзЁїPDAЃЛ
ЃЈ2ЃЉШєЁїOCPгыЁїPDAЕФУцЛ§БШЮЊ1ЃК4ЃЌЂйЧѓБпCPЕФГЄЃЛЂкЧѓБпABЕФГЄЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуOЮЊЪ§жсЕФдЕуЃЌЕуAЁЂBдкЪ§жсЩЯЕФЮЛжУШчЭМЫљЪОЃЌЕуAБэЪОЕФЪ§ЮЊ5ЃЌЯпЖЮABЕФГЄЮЊЯпЖЮOAГЄЕФ1.2БЖ.ЕуCдкЪ§жсЩЯЃЌMЮЊЯпЖЮOCЕФжаЕу

ЃЈ1ЃЉЕуBБэЪОЕФЪ§ЮЊ____________
ЃЈ2ЃЉШєЯпЖЮBMЕФГЄЮЊ4.5ЃЌдђЯпЖЮACЕФГЄЮЊ___________
ЃЈ3ЃЉШєЯпЖЮACЕФГЄЮЊxЃЌЧѓЯпЖЮBMЕФГЄЃЈгУКЌxЕФЪНзгБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌжБЯпyЃНkx+bЃЈkЃЌbЮЊГЃЪ§ЃЉЗжБ№гыxжсЁЂyжсНЛгкЕуAЃЈЉ4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌХзЮяЯпyЃНЉx2+4x+1гыyжсНЛгкЕуCЃЌЕуEдкХзЮяЯпyЃНЉx2+4x+1ЕФЖдГЦжсЩЯвЦЖЏЃЌЕуFдкжБЯпABЩЯвЦЖЏЃЌCE+EFЕФзюаЁжЕЪЧЃЈЁЁЁЁЃЉ

A.2B.4C.2.5D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєШ§ИіЛЅВЛЯрЕШЕФгаРэЪ§МШПЩБэЪОЮЊ1ЃЌa+bЃЌaЕФаЮЪНЃЌгжПЩБэЪОЮЊ0ЃЌ![]() ЃЌbЕФаЮЪНЃЌдђ12a2Љ5abЃН_____ЃЎ
ЃЌbЕФаЮЪНЃЌдђ12a2Љ5abЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЙлВьЬНЫїЃЉгУЁАЃМЁБЁЂЁАЃОЁБЛђЁА=ЁБЭъГЩвдЯТЬюПеЃЌВЂЙлВьСНБпЫуЪНЃЌЬНЫїЙцТЩ:
![]()
![]()
![]()
![]()
ЃЈВТЯыжЄУїЃЉЧыгУвЛИіКЌзжФИaЁЂbЕФЪНзгБэЪОЩЯвдЙцТЩЃЌВЂжЄУїНсТлЕФе§ШЗадЃЛ
ЃЈгІгУЭиеЙЃЉБШНЯДњЪ§ЪНm2-3mn+1гыmn-4n2ЕФДѓаЁЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com