
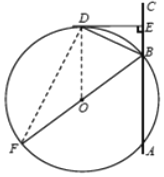
【题目】如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.
(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE=![]() ,求DE的长.
,求DE的长.

【答案】(1)见解析;(2)4.
【解析】
试题分析:(1)先连接OD,根据∠ODB=∠DBE,即可得到OD∥AC,再根据DE⊥AC,可得OD⊥DE,进而得出直线DE是⊙O的切线;
(2)先连接DF,根据题意得到∠F=∠BDE,在Rt△BDF中,根据![]() =sinF=sin∠BDE=
=sinF=sin∠BDE=![]() ,可得BD=2
,可得BD=2![]() ,在Rt△BDE中,根据sin∠BDE=
,在Rt△BDE中,根据sin∠BDE=![]() =
=![]() ,可得BE=2,最后依据勾股定理即可得到DE的长.
,可得BE=2,最后依据勾股定理即可得到DE的长.
试题解析:(1)如图所示,连接OD,
∵OD=OB,∴∠ODB=∠OBD,
∵BD平分∠OBC,∴∠OBD=∠DBE,∴∠ODB=∠DBE,∴OD∥AC,
∵DE⊥AC,∴OD⊥DE,
∵OD是⊙O的半径,∴直线DE是⊙O的切线;
(2)如图,连接DF,
∵BF是⊙O的直径,∴∠FDB=90°,∴∠F+∠OBD=90°,
∵∠OBD=∠DBE,∠BDE+∠DBE=90°,∴∠F=∠BDE,
在Rt△BDF中,![]() =sinF=sin∠BDE=
=sinF=sin∠BDE=![]() ,∴BD=10×
,∴BD=10×![]() =2
=2![]() ,
,
∴在Rt△BDE中,sin∠BDE=![]() =
=![]() ,∴BE=2
,∴BE=2![]() ×
×![]() =2,
=2,
∴在Rt△BDE中,DE=![]() =4.
=4.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】以下问题,不适合普查的是( )
A.学校招聘教师,对应聘人员的面试
B.进入地铁站对旅客携带的包进行的安检
C.调查本班同学的身高
D.调查我国民众对“香港近期暴力”行为的看法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E分别在边BC 和AC上,若AD=AE,则下列结论错误的是( )
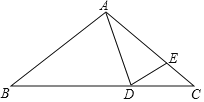
A.∠ADB=∠ACB+∠CAD B.∠ADE=∠AED
C.∠CDE=![]() ∠BAD D.∠AED=2∠ECD
∠BAD D.∠AED=2∠ECD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 A的坐标是(-1,2) .作点A关于x 轴的对称点,得到点A1 ,再将点A1 向下平移 4个单位,得到点A2 ,则点A2 的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=5x2先向右平移3个单位,再向上平移2个单位后,所得的抛物线的解析式为( )
A.y=5(x+3)2+2B.y=5(x+3)2﹣2
C.y=5(x﹣3)2+2D.y=5(x﹣3)2﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com