
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD面积等于6时,求点D的坐标;
(3)点P在线段AM上,当PC与y轴垂直时,过点P作![]() 轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
【答案】(1) ![]() ;M(-1,4);(2)点D的坐标为(-1,-2)或(-1,6).
;M(-1,4);(2)点D的坐标为(-1,-2)或(-1,6).
;(3)点P′不在该抛物线上.
【解析】分析:(1)由抛物线经过的C点坐标以及顶点M的坐标,利用待定系数法即可求出抛物线解析式;
(2)设点D坐标为(﹣1,yD),根据△ACD的面积=6,即可得出关于yD含绝对值符号的一元一次方程,解方程即可得出结论;
(3)作点P关于直线CE的对称点P′,过点P′作PH⊥y轴于H,设P′E交y轴于点N.根据对称的性质即可得出△EON≌△CP′N,从而得出CN=NE,由点A、M的坐标利用待定系数法可求出直线AM的解析式,进而得出点P的坐标.在Rt△P′NC中,由勾股定理可求出CN的值,再由相似三角形的性质以及线段间的关系即可找出点P′的坐标,将其代入抛物线解析式中看等式是否成立,由此即可得出结论.
详解:(1)∵抛物线y=ax2+bx+c经过点C(0,3),顶点为M(﹣1,4),∴ ,解得:
,解得: ,∴所求抛物线的解析式为y=﹣x2﹣2x+3.
,∴所求抛物线的解析式为y=﹣x2﹣2x+3.
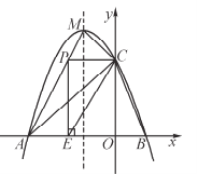
(2)依照题意画出图形,如图1所示.
令y=﹣x2﹣2x+3=0,解得:x=﹣3或x=1,故A(﹣3,0),B(1,0),∴OA=OC,△AOC为等腰直角三角形.
设AC交对称轴x=﹣1于F(﹣1,yF),由点A(﹣3,0)、C(0,3)可知直线AC的解析式为y=x+3,∴yF=﹣1+3=2,即F(﹣1,2).
设点D坐标为(﹣1,yD),则S△ADC=![]() DFAO=
DFAO=![]() ×|yD﹣2|×3=6.
×|yD﹣2|×3=6.
解得:yD=﹣2或yD=6,∴点D的坐标为(﹣1,﹣2)或(﹣1,6).
(3)如图2,点P′为点P关于直线CE的对称点,过点P′作PH⊥y轴于H,设P′E交y轴于点N.
在△EON和△CP′N中,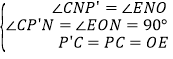 ,∴△EON≌△CP′N(AAS).
,∴△EON≌△CP′N(AAS).
设NC=m,则NE=m.
∵A(﹣3,0)、M(﹣1,4)可知直线AM的解析式为y=2x+6,∴当y=3时,x=﹣![]() ,即点P(﹣
,即点P(﹣![]() ,3),∴P′C=PC=
,3),∴P′C=PC=![]() ,P′N=3﹣m.在Rt△P′NC中,由勾股定理,得:
,P′N=3﹣m.在Rt△P′NC中,由勾股定理,得:![]() +(3﹣m)2=m2,解得:m=
+(3﹣m)2=m2,解得:m=![]() .
.
∵S△P′NC=![]() CNP′H=
CNP′H=![]() P′NP′C,∴P′H=
P′NP′C,∴P′H=![]() .
.
由△CHP′∽△CP′N可得:![]() ,∴CH=
,∴CH=![]() =
=![]() ,∴OH=3﹣
,∴OH=3﹣![]() =
=![]() ,∴P′的坐标为(
,∴P′的坐标为(![]() ).
).
将点P′(![]() )代入抛物线解析式,得:y=﹣
)代入抛物线解析式,得:y=﹣![]() ﹣2×
﹣2×![]() +3=
+3=![]() ≠
≠![]() ,∴点P′不在该抛物线上.
,∴点P′不在该抛物线上.



 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
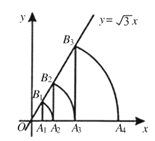
【题目】如图,已知直线y=![]() x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点A6的坐标为____________.
x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点A6的坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的![]() 倍;用
倍;用![]() 元单独购买甲种图书比单独购买乙种图书要少
元单独购买甲种图书比单独购买乙种图书要少![]() 本.
本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共![]() 本,且投入的经费不超过
本,且投入的经费不超过![]() 元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实根,且其中一个根为另一根的2倍,则称这样的方程为“倍根方”,以下关于倍根方程的说法正确的是______(填正确序号)
①方程x2﹣x﹣2=0是倍根方程.
②若(x﹣2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0.
③若点(p,q)在反比例函数y=![]() 的图象上,则关于x的方程px2+3x+q=0是倍根方程.
的图象上,则关于x的方程px2+3x+q=0是倍根方程.
④若方程ax2+bx+c=0是倍根方程且相异两点M(1+t,s)、N(4﹣t,s)都在抛物线y=ax2+bx+c上,则方程ax2+bx+c=0必有一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
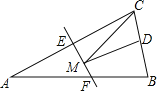
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交x轴于点B(2,0),交y轴于点A(0,2),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=3,连接DA,∠DAC=90°.
(1)求直线AB的解析式.
(2)求D点坐标及过O、D、B三点的抛物线解析式.
(3)若点P是线段OB上的动点,过点P作x轴的垂线交AB于F,交(2)中抛物线于E,连CE,是否存在P使△BPF与△FCE相似?若存在,请求出P点坐标;若不存在说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花园内有一块边长为a的正方形土地,园艺师设计了四种不同的图案,如下图的A、B、C、D所示,其中的阴影部分用于种植花草.种植花草部分面积最大的图案是( )(说明:A、B、C中圆弧的半径均为![]() ,D中圆弧的半径为a)
,D中圆弧的半径为a)
A.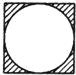 B.
B.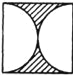 C.
C.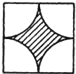 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
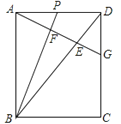
【题目】如图,在长方形![]() 中,
中, ![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)当![]() =
=![]() ,且
,且![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() =
=![]() .
.
(2)在(1)的条件下,求![]() 的值;
的值;
(3)类比探究:若![]() =3
=3![]() ,
, ![]() =2
=2![]() ,则
,则![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com