
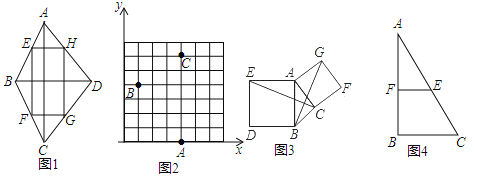
����Ŀ����ͼ1����˳�������ı���ABCD�����е�õ��ı���EFGH�Ǿ��Σ����ԭ�ı���ABCDΪ����ĸ���Ρ������ı��εĶԽ����ഹֱ����ô����ı��γ�Ϊ����ĸ���Ρ�.
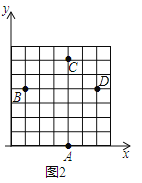
��1����ͼ2����ֱ������ϵxOy�У���֪A��4��0����B��1��4����C��4��6�������ڸ���ϱ��D���λ�ã�ֻ��һ�㼴�ɣ���ʹ�ı���ABCD����ĸ����.��д����D������.
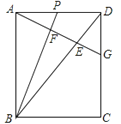
��2����ͼ3���ԡ�ABC�ı�AB��ACΪ�ߣ�������������������ABDE��ACFG������CE��BG�ཻ�ڵ�O�����ж��ı���BEGC����ĸ���Σ�˵������.
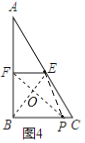
��3����ͼ4����Rt��ABC�У�AB��8��BC��6��E��б��AC���е㣬F��ֱ�DZ�AB���е㣬P��ֱ�DZ�BC��һ���㣬��̽������PC��_____ʱ���ı���BPEF����ĸ���Σ���ֱ���������У�30������Ե�ֱ�DZ���б�ߵ�һ�룩
���𰸡���1��ͼ���������D��6��4������2�������������3��![]() .
.
��������
��1��������ĸ���εĶ�������ó���BD��x��ʱ��D���߶�AC�Ҳ༴�ɣ���2�����������ε����ʽ��ȫ�������ε��ж������ó���EAC�ա�GAB��SAS���������ó�EC��BG���ó��𰸼��ɣ���3��������λ�ߵ����ʿɵ�EF�ij������á���ĸ���Ρ��Ķ��������������ε��������ж��ɵó�BP�ij��������ɵ�PC�ij�.
��1����ͼ2��ʾ����D��Ϊ����D��6��4����
��2����ͼ3��
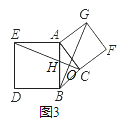
���ı���ABDE��ACFG�������Σ�
���EAB����GAC��90�㣬AG��AC��AE��AB��
���EAC����EAB����BAC����GAC����BAC����GAB
�ڡ�EAC�͡�GAB��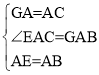
���EAC�ա�GAB��SAS����
���ABG����AEC��
���AEC����AHE����ABG����BHO��90�㣬
��EC��BG��
���ı���BEGC����ĸ���Σ�
��3����ͼ4������BE����FP��BE��O����BC��P������EP��
���ı���BPEF����ĸ���Σ�
�ߡ�FPB����BFP��90�㣬��EBF����BFP��90�㣬
���FPB����FBE��
��E��б��AC���е㣬F��ֱ�DZ�AB���е㣬
��EF//BC��BF��![]() AB=4��EF��
AB=4��EF��![]() BC=3��
BC=3��
����FBC=90����
����EFB=180��-90��=90����
����EFB=��FBP=90��
���BFE�ס�PBF��
��![]() ��
��
��![]()
��PC=BC-BP=6-![]() =
=![]()
����P��BC���ϣ�PC=![]() ʱ���ı���BPEF����ĸ����.
ʱ���ı���BPEF����ĸ����.
�ʴ�Ϊ��![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
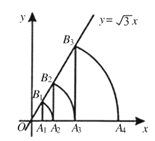
����Ŀ����ͼ����ֱ֪��y��![]() x����A1������Ϊ(1��0)������A1��x��Ĵ��߽�ֱ���ڵ�B1����ԭ��OΪԲ�ģ�OB1�ij�Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2�ij�Ϊ�뾶������x���ڵ�A3��������������������ȥ������A6������Ϊ____________��
x����A1������Ϊ(1��0)������A1��x��Ĵ��߽�ֱ���ڵ�B1����ԭ��OΪԲ�ģ�OB1�ij�Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2�ij�Ϊ�뾶������x���ڵ�A3��������������������ȥ������A6������Ϊ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��x���ڵ�B��2��0������y���ڵ�A��0��2����ֱ��DM��x���������ڵ�M�����߶�AB�ڵ�C��DM=3������DA����DAC=90����
��1����ֱ��AB�Ľ���ʽ��
��2����D�����꼰��O��D��B����������߽���ʽ��
��3������P���߶�OB�ϵĶ��㣬����P��x��Ĵ��߽�AB��F������2������������E����CE���Ƿ����Pʹ��BPF����FCE���ƣ������ڣ������P�����ꣻ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ��߳�Ϊa�����������أ���ʦ��������ֲ�ͬ��ͼ��������ͼ��A��B��C��D��ʾ�����е���Ӱ����������ֲ���ݣ���ֲ���ݲ����������ͼ���ǣ���������˵����A��B��C��Բ���İ뾶��Ϊ![]() ��D��Բ���İ뾶Ϊa��
��D��Բ���İ뾶Ϊa��
A.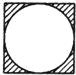 B.
B.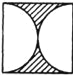 C.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
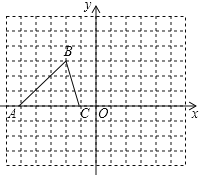
����Ŀ����֪��ABC���������������ֱ�ΪA����5��0����B����2��3����C����1��0��
��1��������ABC��������ԭ��O�����ĶԳƵġ�![]() ��
��
��2������ABC������ԭ��O˳ʱ����ת90�㣬������Ӧ�ġ�![]() ��
��
��3������![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊƽ���ı��Σ���ֱ��д���ڵ��������е�
Ϊ������ı���Ϊƽ���ı��Σ���ֱ��д���ڵ��������е�![]() ����____��
����____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ļ�����.
-4��![]() ��0��
��0��![]() ��-3.14��717��-��+5����+1.88��
��-3.14��717��-��+5����+1.88��![]()
��1���������ϣ��� �� ����
��2���������ϣ��� ������
��3���������ϣ��� ������
��4���������ϣ��� �� ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b�DZ�ʾ������ͬ��A��B������������|a|��5��|b|��2�������������λ����ͼ��ʾ.
![]()
(1)��ȷ��a��b��ֵ�������ʾa��b�����ĵ�ľ��룻
(2)����C�������ϣ���C����A�ľ����ǵ�C����B�����3�������C��ʾ����Ϊ_ ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����![]() �У�
�� ![]() ��
��![]() ����һ���㣬����
����һ���㣬����![]() ������
������![]() ��
��![]() �Ĵ��ߣ�����Ϊ
�Ĵ��ߣ�����Ϊ![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() .
.
��1����![]() ��
��![]() ����
����![]() ��
��![]() ���е�ʱ����֤��
���е�ʱ����֤�� ![]() ��
��![]() .
.
��2���ڣ�1���������£���![]() ��ֵ��
��ֵ��
��3�����̽������![]() ��3
��3![]() ��
�� ![]() ��2
��2![]() ����
����![]() �� .
�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˽�ij��������������ˮ��ʼʵ�н���ʽ����ˮ��,ʵ�еĽ���ʽ����ˮ�۷�Ϊ����(��ˮ�����ѡ����������ѵ�����)�����±���ʾ��
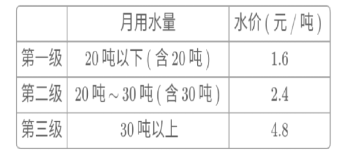
������ij�û�2016��9�·ݵ���ˮ��Ϊ35��,������������Ӧ��ˮ��Ϊ��20��1.6+10��2.4+(352010)��4.8=80(Ԫ)
(1)���С��2016��6�·ݵ���ˮ��Ϊ10�֣�����ɽ�ˮ��___Ԫ��
(2)���С����2016��7�·ݽɽ�ˮ��44Ԫ����ôС����2016��7�·ݵ���ˮ��Ϊ���ٶ�?
(3)���С����2016��8�·ݵ���ˮ��Ϊa��,��ô��С���Ҹ���Ӧ�ɽ�ˮ�Ѷ���Ԫ?(�ú�a�Ĵ���ʽ��ʾ)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com