
����Ŀ�����˽�ij��������������ˮ��ʼʵ�н���ʽ����ˮ��,ʵ�еĽ���ʽ����ˮ�۷�Ϊ����(��ˮ�����ѡ����������ѵ�����)�����±���ʾ��
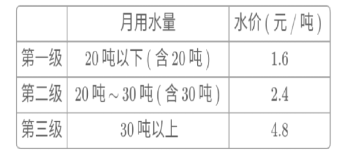
������ij�û�2016��9�·ݵ���ˮ��Ϊ35��,������������Ӧ��ˮ��Ϊ��20��1.6+10��2.4+(352010)��4.8=80(Ԫ)
(1)���С��2016��6�·ݵ���ˮ��Ϊ10�֣�����ɽ�ˮ��___Ԫ��
(2)���С����2016��7�·ݽɽ�ˮ��44Ԫ����ôС����2016��7�·ݵ���ˮ��Ϊ���ٶ�?
(3)���С����2016��8�·ݵ���ˮ��Ϊa��,��ô��С���Ҹ���Ӧ�ɽ�ˮ�Ѷ���Ԫ?(�ú�a�Ĵ���ʽ��ʾ)
���𰸡���1��16����2��25�֣���3��4.8a88Ԫ.
��������
��1���жϵõ�10��Ϊ20�����£��ɱ����е�ˮ�ۼ��㼴�ɵõ������
��2���жϵ�7�·���ˮ����20��-30��֮�䣬��Ϊx�֣�����ˮ���г����̣�������̵Ľ⼴�ɵõ������
��3������a�ķ�Χ�����յ�3���շѷ�ʽ�����㼴�ɵõ������
(1)��10<20��
��������ˮ��Ϊ10��1.6=16(Ԫ)��
�ʴ�Ϊ��16��
(2).��20��1.6=32(Ԫ)��20��1.6+10��2.4=56(Ԫ)
��32<44<56
��С����2016��7�·ݽɽ�ˮ�����ڵڶ���
��С����2016��7�·ݵ���ˮ��Ϊx�֣��������⣬�ã�
20��1.6+2.4(x20)=44
��ã�x=25
��С����2016��7�·ݵ���ˮ��Ϊ25�֣�
(3).��0a20ʱ������Ӧ�ɽ�ˮ��Ϊ1.6aԪ��
��20a30ʱ,����Ӧ�ɽ�ˮ��Ϊ1.6��20+2.4(a20)=2.4a16Ԫ��
��a30ʱ,����Ӧ�ɽ�ˮ��Ϊ1.6��20+2.4��10+4.8(a30)=4.8a88Ԫ.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
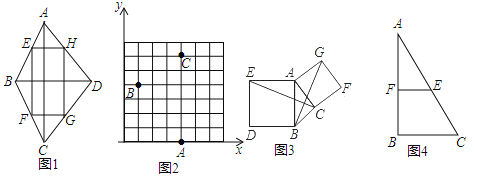
����Ŀ����ͼ1����˳�������ı���ABCD�����е�õ��ı���EFGH�Ǿ��Σ����ԭ�ı���ABCDΪ����ĸ���Ρ������ı��εĶԽ����ഹֱ����ô����ı��γ�Ϊ����ĸ���Ρ�.
��1����ͼ2����ֱ������ϵxOy�У���֪A��4��0����B��1��4����C��4��6�������ڸ���ϱ��D���λ�ã�ֻ��һ�㼴�ɣ���ʹ�ı���ABCD����ĸ����.��д����D������.
��2����ͼ3���ԡ�ABC�ı�AB��ACΪ�ߣ�������������������ABDE��ACFG������CE��BG�ཻ�ڵ�O�����ж��ı���BEGC����ĸ���Σ�˵������.
��3����ͼ4����Rt��ABC�У�AB��8��BC��6��E��б��AC���е㣬F��ֱ�DZ�AB���е㣬P��ֱ�DZ�BC��һ���㣬��̽������PC��_____ʱ���ı���BPEF����ĸ���Σ���ֱ���������У�30������Ե�ֱ�DZ���б�ߵ�һ�룩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OΪ�����ԭ�㣬��A��B�������ϵ�λ����ͼ��ʾ����A��ʾ����Ϊ5���߶�AB�ij�Ϊ�߶�OA����1.2��.��C�������ϣ�MΪ�߶�OC���е�

��1����B��ʾ����Ϊ____________
��2�����߶�BM�ij�Ϊ4.5�����߶�AC�ij�Ϊ___________
��3�����߶�AC�ij�Ϊx�����߶�BM�ij����ú�x��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABD�У�AB��AD��1����B��30������ABD����A����ʱ������0��������120������ת�õ���ACE��CE��AD��BD�ֱ��ڵ�G��F��AD��CE���ڵ�G����DF+GF��x����AEG�����Ϊy����y����x�ĺ�������ʽΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȵ��������ȿɱ�ʾΪ1��a+b��a����ʽ���ֿɱ�ʾΪ0��![]() ��b����ʽ����12a2��5ab��_____��
��b����ʽ����12a2��5ab��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ƽ���ĵ����ϣ������ɸ���ȫ��ͬ���ⳤΪ10 cm��С������ѳ�һ��������.
��1�����Ѹ������������ĸ���ͼ(��ͼ��)�����㻭����������������ͼ������ͼ;
��2������������ͷ����һЩ��ͬ��С�����壬���������������������ͼ����ͼ����.
����ͼ����ʾ�ļ������������������Ӽ���С������?
����ͼ����ʾ�ļ�������������������С������?
���ڢڵ�����£�����������������ǽ�ǣ���ͼ����ʾ�Ǵ�ʱ�����������õĸ���ͼ���������������������Ϻ��ᣬ����Ҫ�������������Ƕ���?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���������ϵ�A��ʾ��������Ϊ-6����B��ʾ��������Ϊ4����P�ӵ�A��������ÿ��2����λ���ȵ��ٶ������������B�˶�������P�����B���������أ���Ȼ��ÿ��2����λ���ȵ��ٶ��˶�����Aֹͣ�����˶�ʱ��Ϊt����λ���룩��
��1����t=1ʱ��P��ʾ����������
��2�����P���B�غ�ʱ��tֵ��
��3���ڵ�P�������ɵ�A����B�ٻص���A���˶������У����P���A�ľ��루�ú�t�Ĵ���ʽ��ʾ����
��4������P��ʾ����������ԭ��ľ�����2����λ����ʱ��ֱ��д����������������tֵ.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����������������˾ӳɶ�����������һ���㳡����ֲ�ס������ֻ���.���г����飬���ֻ��ܵ���ֲ����![]() ��Ԫ������ֲ���
��Ԫ������ֲ���![]() ֮��ĺ�����ϵ��ͼ��ʾ�����ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ.
֮��ĺ�����ϵ��ͼ��ʾ�����ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ.
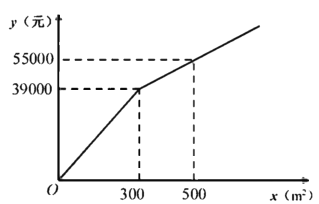
��1��ֱ��д����![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���㳡�ϼס������ֻ��ܵ���ֲ�����![]() �������ֻ��ܵ���ֲ���������
�������ֻ��ܵ���ֲ���������![]() ���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�������٣������ܷ���Ϊ����Ԫ��
���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�������٣������ܷ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ӳֽ�������������ӣ�ÿ��������3�����β����2���������ε�����ɡ�Ӳֽ������ͼ���ַ�ʽ�ü����ü���߽��ϲ������ã�
A��������6�����棻 B��������4�������5�����档

����19��Ӳֽ�壬�ü�ʱ![]() ����A������������B������
����A������������B������
��1����![]() �Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
�Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
��2�����ü����IJ���͵���ǡ��ȫ�����꣬���������ٸ����ӣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com