
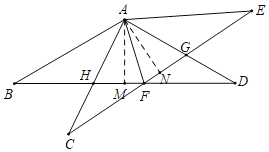
【题目】已知,如图,△ABD中,AB=AD=1,∠B=30°,△ABD绕着A点逆时针α(0°<α<120°)旋转得到△ACE.CE与AD、BD分别交于点G、F;AD、CE交于点G,设DF+GF=x,△AEG的面积为y,则y关于x的函数解析式为_____.

【答案】y=![]() (0<x<
(0<x<![]() ).
).
【解析】
设AC交BD于H,作AM⊥BD于M,AN⊥EC于N.想办法证明FG+DF=DH,求出BD,AM即可解决问题.
解:设AC交BD于H,作AM⊥BD于M,AN⊥EC于N.
∵AB=AD=1,∠B=30°,AM⊥BD,
∴AM=![]() AN=
AN=![]() ,BM=DM=
,BM=DM=![]() ,
,
∴BD=EC=![]() ,
,
∵∠BAD=∠CAE,
∴∠BAH=∠EAG,
∵AB=AE,∠B=∠E=30°,
∴△BAH≌△EAG(ASA),
∴AH=AG,BH=EG,
∵△ABD≌△ACE,
∴AM=AN,
∵∠AMH=∠ANG=90°,
∴Rt△AMH≌Rt△ANG(HL),
∴HM=GN,
∵∠AMF=∠ANF=90°,AF=AF,
∴Rt△AFM≌Rt△AFN(HL),
∴FM=FN,
∴FG=FH,
∴FG+DF=FH+DF=DH=x,
∴EG=BH=![]() ﹣x,
﹣x,
∴y=S△AEG=![]() EGAN=
EGAN=![]() ,
,
∴y=![]() (0<x<
(0<x<![]() ),
),
故答案为y=![]() (0<x<
(0<x<![]() ).
).


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】花园内有一块边长为a的正方形土地,园艺师设计了四种不同的图案,如下图的A、B、C、D所示,其中的阴影部分用于种植花草.种植花草部分面积最大的图案是( )(说明:A、B、C中圆弧的半径均为![]() ,D中圆弧的半径为a)
,D中圆弧的半径为a)
A.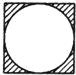 B.
B.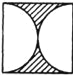 C.
C.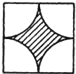 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
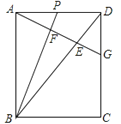
【题目】如图,在长方形![]() 中,
中, ![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)当![]() =
=![]() ,且
,且![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() =
=![]() .
.
(2)在(1)的条件下,求![]() 的值;
的值;
(3)类比探究:若![]() =3
=3![]() ,
, ![]() =2
=2![]() ,则
,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,列一元一次方程解应用题,回答下列问题:
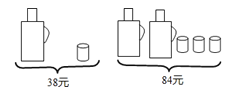
(1)求一个暖瓶与一个水杯分别是多少元?
(2)若买3个暖瓶与4个水杯一共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据了解某市区居民生活用水开始实行阶梯式计量水价,实行的阶梯式计量水价分为三级(污水处理费、垃圾处理费等另计),如下表所示:
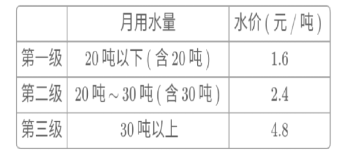
例:若某用户2016年9月份的用水量为35吨,按三级计算则应交水费为:20×1.6+10×2.4+(352010)×4.8=80(元)
(1)如果小白家2016年6月份的用水量为10吨,则需缴交水费___元;
(2)如果小明家2016年7月份缴交水费44元,那么小明家2016年7月份的用水量为多少吨?
(3)如果小明家2016年8月份的用水量为a吨,那么则小明家该月应缴交水费多少元?(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一段圆柱体的树干的示意图,已知树干的半径r=10cm,AD=45cm. (π值取3)
(1)若螳螂在点A处,蝉在点C处,图1中画出了螳螂捕蝉的两条路线,即A→D→C和A→C,图2是该圆柱体的侧面展开图,判断哪条路的距离较短,并说明理由;
(2)若螳螂在点A处,蝉在点D处,螳螂想要捕到这只蝉,但又怕蝉发现,于是螳螂绕到
后方去捕捉它,如图3所示,求螳螂爬行的最短距离;(提示: ![]() =75)
=75)
(3)图4是该圆柱体的侧面展开图,蝉N在半径为10cm的⊙O的圆上运动,⊙O与BC相切,点O到CD的距离为20cm,螳螂M在线段AD运动上,连接MN,MN即为螳螂捕蝉时螳螂爬行的距离,若要使MN与⊙O总是相切,求MN的长度范围.

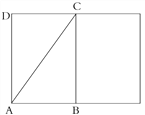


图1 图2 图3 图4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com