
【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C所在位置的深度.(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

科目:初中数学 来源: 题型:
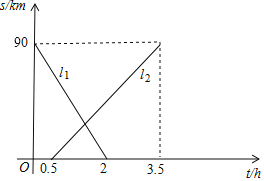
【题目】如图表示甲和乙沿相同路线相向行驶,![]() ,
,![]() 表示两人离
表示两人离![]() 地行驶的路程
地行驶的路程![]() (千米)与经过的时间
(千米)与经过的时间![]() (小时)之间的函数关系.甲先出发,
(小时)之间的函数关系.甲先出发,![]() 两地相距90千米.请根据这个行驶过程中的图象填空:
两地相距90千米.请根据这个行驶过程中的图象填空:
(1)表示甲离![]() 地的距离与时间的关系的图象是 (填
地的距离与时间的关系的图象是 (填![]() 或
或![]() ),甲的速度是 ,乙的速度是: .
),甲的速度是 ,乙的速度是: .
(2)甲出发多少时间两人恰好相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
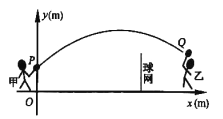
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在![]() 点上正方
点上正方![]() 的
的![]() 处发出一球,羽毛球飞行的高度
处发出一球,羽毛球飞行的高度![]() 与水平距离
与水平距离![]() 之间满足函数表达式
之间满足函数表达式![]() .已知点
.已知点![]() 与球网的水平距离为
与球网的水平距离为![]() ,球网的高度为
,球网的高度为![]() .
.
(1)当![]() 时,①求
时,①求![]() 的值.②通过计算判断此球能否过网.
的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到点![]() 的水平距离为
的水平距离为![]() ,离地面的高度为
,离地面的高度为![]() 的
的![]() 处时,乙扣球成功,求
处时,乙扣球成功,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
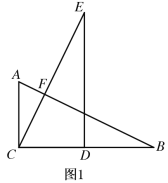
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK
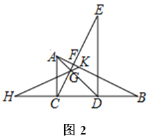
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,则下列说法正确的是( )
(分钟)之间的函数关系如图所示,则下列说法正确的是( )
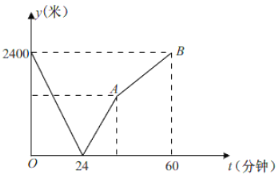
①当![]() 分钟时甲乙两人相遇;
分钟时甲乙两人相遇;
②甲的速度为40米/分钟;
③乙的速度为50米/分钟;
④乙到达目的地时,甲离目的地的距离为800米.
A.①②B.③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AB=9,cosA=![]() ,如果将△ABC绕着点C旋转至△A′B′C′的位置,使点B′落在∠ACB的角平分线上,A′B′与AC相交于点D,那么线段CD的长等于______.
,如果将△ABC绕着点C旋转至△A′B′C′的位置,使点B′落在∠ACB的角平分线上,A′B′与AC相交于点D,那么线段CD的长等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com