
【题目】有一艘渔轮在海上C处作业时,发生故障,立即向搜救中心发出救援信号,此时搜救中心的两艘救助轮救助一号和救助二号分别位于海上A处和B处,B在A的正东方向,且相距100里,测得地点C在A的南偏东60,在B的南偏东30方向上,如图所示,若救助一号和救助二号的速度分别为40里/小时和30里/小时,问搜救中心应派那艘救助轮才能尽早赶到C处救援?(![]() ≈1.7)
≈1.7)
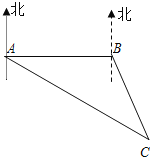
【答案】搜救中心应派2号艘救助轮才能尽早赶到C处救援
【解析】
作CD⊥AB交AB延长线于D,由等腰三角形的判定与性质求出BC的长,根据勾股定理分别计算出CD和AC的长度,利用速度、时间、路程之间的关系求出各自的时间比较大小即可.
解:作CD⊥AB交AB延长线于D,
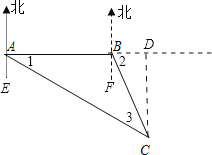
由已知得:∠EAC=60°,∠FBC=30°,
∴∠1=30°,∠2=90°-30°=60°,
∵∠1+∠3=∠2,
∴∠1=∠3,
∴AB=BC=100里,
在Rt△BDC中,BD=![]() BC=50里,
BC=50里,
∴CD=![]() 里,
里,
∵AD=AB+BD=150里,
∴在Rt△ACD中,AC=![]() 里,
里,
∵![]() ≈4.25小时,
≈4.25小时,![]() 小时,且
小时,且![]() <4.25,
<4.25,
∴搜救中心应派2号艘救助轮才能尽早赶到C处救援.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与射线
长为半径画弧,与射线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() ,垂足为
,垂足为![]() .
.

(1)线段![]() 与图中现有的哪一条线段相等?你得出的结论是:
与图中现有的哪一条线段相等?你得出的结论是:![]() ;
;
(2)证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=10,sin∠BAC=![]() ,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
(1)求证:∠ABE=∠CAD.
(2)如图,当点G在线段AD上时,求y关于x的函数解析式及定义域.
(3)若△DFG是直角三角形,求△CEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.
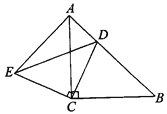
求证:
(1)△ACE≌△BCD;
(2)AE⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
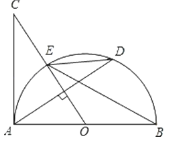
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与半圆O交于点E,连接BE,DE.
(1)求证:∠BED=∠C;
(2)若OA=5,AD=8,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com