
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与半圆O交于点E,连接BE,DE.
(1)求证:∠BED=∠C;
(2)若OA=5,AD=8,求AC的长.
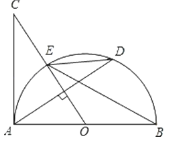
【答案】(1)证明见解析;(2)AC=![]() .
.
【解析】
(1)由切线的性质得∠1+∠2=90°;由同角的余角相等得到∠C=∠2.由圆周角定理知∠BED=∠2,故∠BED=∠C;
(2)连接BD.由直径直径对的圆周角是直角得∠ADB=90°,由勾股定理求得BD=![]() =
=![]() =6,由△OAC∽△BDA得OA:BD=AC:DA,从而求得AC的值.
=6,由△OAC∽△BDA得OA:BD=AC:DA,从而求得AC的值.
(1)证明:∵AC是⊙O的切线,AB是⊙O直径,
∴AB⊥AC.
则∠1+∠2=90°,
又∵OC⊥AD,
∴∠1+∠C=90°,
∴∠C=∠2,
而∠BED=∠2,
∴∠BED=∠C;
(2)解:连接BD,
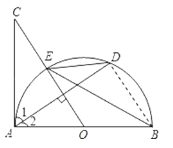
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD=![]() =
=![]() =6,
=6,
∴△OAC∽△BDA,
∴OA:BD=AC:DA,
即5:6=AC:8,
∴AC=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】今年某市水果大丰收,![]() 两个水果基地分别收获同种水果
两个水果基地分别收获同种水果![]() 件、
件、![]() 件,现需把这些水果全部运往甲、乙两销售点,从
件,现需把这些水果全部运往甲、乙两销售点,从![]() 基地运往甲、乙两销售点的费用分别为每件
基地运往甲、乙两销售点的费用分别为每件![]() 元和
元和![]() 元,从
元,从![]() 基地运往甲、乙两销售点的费用分别为每件
基地运往甲、乙两销售点的费用分别为每件![]() 元和
元和![]() 元,现甲销售点需要水果
元,现甲销售点需要水果![]() 件,乙销售点需要水果
件,乙销售点需要水果![]() 件.
件.
![]() 设从
设从![]() 基地运往甲销售点水果
基地运往甲销售点水果![]() 件,总运费为
件,总运费为![]() 元,请用含的
元,请用含的![]() 代数式表示
代数式表示![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
![]() 若总运费不超过
若总运费不超过![]() 元,且
元,且![]() 基地运往甲销售点的水果不低于
基地运往甲销售点的水果不低于![]() 件,试确定运费最低的运输方案,并求出最低运费.
件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
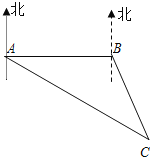
【题目】有一艘渔轮在海上C处作业时,发生故障,立即向搜救中心发出救援信号,此时搜救中心的两艘救助轮救助一号和救助二号分别位于海上A处和B处,B在A的正东方向,且相距100里,测得地点C在A的南偏东60,在B的南偏东30方向上,如图所示,若救助一号和救助二号的速度分别为40里/小时和30里/小时,问搜救中心应派那艘救助轮才能尽早赶到C处救援?(![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材原题解答:
已知![]() 是含字母
是含字母![]() 的单项式,要使多项式
的单项式,要使多项式![]() 是某个多项式的平方,求
是某个多项式的平方,求![]() .
.
解:根据完全平方公式,分两种情况:
当![]() 为含字母
为含字母![]() 的一次单项式时,
的一次单项式时,
![]()
![]() .
.
当![]() 为含字母
为含字母![]() 的四次单项式时,
的四次单项式时,
则![]()
![]() 为
为![]() 或
或![]() 或
或![]()
问题发现:
由上面问题解答过程,我们可以得到下列等式:
![]() .
.
观察等式的左边多项式的系数发现:![]() .
.
爱学习的小明又进行了很多运算:![]() 等等,
等等,
发现同样有![]() .
.
于是小明猜测:若多项式![]() (
(![]() 是常数,
是常数,![]() )是某个含
)是某个含![]() 的多项式的平方,则系数
的多项式的平方,则系数![]() 一定存在某种关系
一定存在某种关系
问题解决:
(1)请用代数式表示![]() 之间的关系;
之间的关系;
(2)若多项式![]() 加上一个含字母y的单项式,就能变形为一个含
加上一个含字母y的单项式,就能变形为一个含![]() 的多项式的平方,请直接写出所有满足条件的单项式,
的多项式的平方,请直接写出所有满足条件的单项式,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).

(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3x2)(x3y)2;
(2)(x﹣5)(2x+1);
(3)(a﹣2)2﹣(a﹣1)(a+1);
(4)(3a﹣b+![]() )(3a﹣b﹣
)(3a﹣b﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在坡角为30°的山坡上有一竖立的旗杆AB,其正前方矗立一墙,当阳光与水平线成45°角时,测得旗杆AB落在坡上的影子BD的长为8米,落在墙上的影子CD的长为6米,求旗杆AB的高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
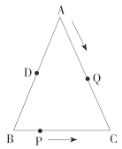
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 移动,同时点
移动,同时点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 以
以![]() 的速度移动,若
的速度移动,若![]() 、
、![]() 同时出发,当有一个点移动到点
同时出发,当有一个点移动到点![]() 时,
时,![]() 、
、![]() 都停止运动,设
都停止运动,设![]() 、
、![]() 移动时间为
移动时间为![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)当![]() 时,问
时,问![]() 与
与![]() 是否全等,并说明理由.
是否全等,并说明理由.
(3)![]() 时,若
时,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com