
【题目】已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.
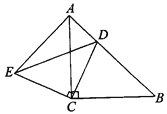
求证:
(1)△ACE≌△BCD;
(2)AE⊥AB.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)利用等腰直角三角形的性质求得∠BCD=ECA ,BC=CA,CD=CE,然后根据SAS即可证明;
(2)利用等腰直角三角形和全等三角形的性质得到∠B=∠CAB=45°,∠CAE=∠CBD=45°,从而证明∠DAE=90°即可.
解:(1)∵△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,
∴∠ACB-∠ACD=∠DCE-∠ACD
∴∠BCD=ECA ,BC=CA,CD=CE,
在△ACE和△BCD中,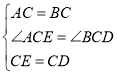 ,
,
∴△ACE≌△BCD.
(2)∵△ABC和△ECD都是等腰直角三角形
∴BC=AC,∠ACB=90°,
∴∠B=∠CAB=45°
∵△ACE≌△BCD,
∴∠CAE=∠CBD=45°,
∴∠DAE=∠CAB+∠CAE=90°,
∴AE⊥AB.



科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据重庆轨道集团提供的日客运量统计,2019年2月21日重庆轨道交通首次日客运量突破300万乘次,其中近期开通的重庆轨道交通环线日客运量为21.5万乘次.据了解,某工作日上午7点至9点轨道环线四公里站有20列列车进出站,每列车进出站时,将上车和下车的人数记录下来,各得到20个数据,并将数据进行整理,绘制成了如下两幅不完整统计图.(数据分组为:![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() )
)
I.上车人数在![]() 组的是:190,190,191,192,193,193,195,196,198,198,198,198;
组的是:190,190,191,192,193,193,195,196,198,198,198,198;
II.上车人数的平均数、中位数如下表:
平均数 | 中位数 | |
上车人数(人) | 194 | a |
根据以上信息,回答下列问题:
(1)请补全频数分布直方图;
(2)表中![]() ________,扇形统计图中
________,扇形统计图中![]() _________,扇形统计图中
_________,扇形统计图中![]() 组所在的圆心角度数为________度;
组所在的圆心角度数为________度;
(3)请利用平均数,估算一周内5个工作日的上午7点至9点重庆轨道环线四公里站的上车总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
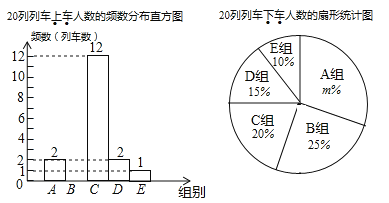
【题目】有一艘渔轮在海上C处作业时,发生故障,立即向搜救中心发出救援信号,此时搜救中心的两艘救助轮救助一号和救助二号分别位于海上A处和B处,B在A的正东方向,且相距100里,测得地点C在A的南偏东60,在B的南偏东30方向上,如图所示,若救助一号和救助二号的速度分别为40里/小时和30里/小时,问搜救中心应派那艘救助轮才能尽早赶到C处救援?(![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
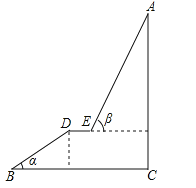
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材原题解答:
已知![]() 是含字母
是含字母![]() 的单项式,要使多项式
的单项式,要使多项式![]() 是某个多项式的平方,求
是某个多项式的平方,求![]() .
.
解:根据完全平方公式,分两种情况:
当![]() 为含字母
为含字母![]() 的一次单项式时,
的一次单项式时,
![]()
![]() .
.
当![]() 为含字母
为含字母![]() 的四次单项式时,
的四次单项式时,
则![]()
![]() 为
为![]() 或
或![]() 或
或![]()
问题发现:
由上面问题解答过程,我们可以得到下列等式:
![]() .
.
观察等式的左边多项式的系数发现:![]() .
.
爱学习的小明又进行了很多运算:![]() 等等,
等等,
发现同样有![]() .
.
于是小明猜测:若多项式![]() (
(![]() 是常数,
是常数,![]() )是某个含
)是某个含![]() 的多项式的平方,则系数
的多项式的平方,则系数![]() 一定存在某种关系
一定存在某种关系
问题解决:
(1)请用代数式表示![]() 之间的关系;
之间的关系;
(2)若多项式![]() 加上一个含字母y的单项式,就能变形为一个含
加上一个含字母y的单项式,就能变形为一个含![]() 的多项式的平方,请直接写出所有满足条件的单项式,
的多项式的平方,请直接写出所有满足条件的单项式,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3x2)(x3y)2;
(2)(x﹣5)(2x+1);
(3)(a﹣2)2﹣(a﹣1)(a+1);
(4)(3a﹣b+![]() )(3a﹣b﹣
)(3a﹣b﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com