
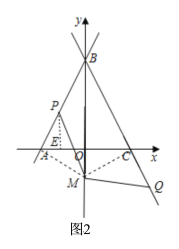
【题目】如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且AB=BC.
(1)求直线BC的解析式;
(2)点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);
(3)在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.
【答案】(1)y=﹣2x+6;(2)点P(m﹣6,2m﹣6);(3)y=﹣x+![]()
【解析】
(1)先求出点A,点B坐标,由等腰三角形的性质可求点C坐标,由待定系数法可求直线BC的解析式;
(2)证明△PGA≌△QHC(AAS),则PG=HQ=2m﹣6,故点P的纵坐标为:2m﹣6,而点P在直线AB上,即可求解;
(3)由“SSS”可证△APM≌△CQM,△ABM≌△CBM,可得∠PAM=∠MCQ,∠BQM=∠APM=45°,∠BAM=∠BCM,由“AAS”可证△APE≌△MAO,可得AE=OM,PE=AO=3,可求m的值,进而可得点P,点Q的坐标,即可求直线PQ的解析式.
(1)∵直线y=2x+6与x轴交于点A,与y轴交于点B,
∴点B(0,6),点A(﹣3,0),
∴AO=3,BO=6,
∵AB=BC,BO⊥AC,
∴AO=CO=3,
∴点C(3,0),
设直线BC解析式为:y=kx+b,则![]() ,解得:
,解得:![]() ,
,
∴直线BC解析式为:y=﹣2x+6;
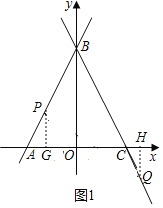
(2)如图1,过点P作PG⊥AC于点G,过点Q作HQ⊥AC于点H,
∵点Q横坐标为m,
∴点Q(m,﹣2m+6),
∵AB=CB,
∴∠BAC=∠BCA=∠HCQ,
又∵∠PGA=∠QHC=90°,AP=CQ,
∴△PGA≌△QHC(AAS),
∴PG=HQ=2m﹣6,
∴点P的纵坐标为:2m﹣6,
∵直线AB的表达式为:y=2x+6,
∴2m﹣6=2x+6,解得:x=m﹣6,
∴点P(m﹣6,2m﹣6);
(3)如图2,连接AM,CM,过点P作PE⊥AC于点E,
∵AB=BC,BO⊥AC,
∴BO是AC的垂直平分线,
∴AM=CM,且AP=CQ,PM=MQ,
∴△APM≌△CQM(SSS)
∴∠PAM=∠MCQ,∠BQM=∠APM=45°,
∵AM=CM,AB=BC,BM=BM,
∴△ABM≌△CBM(SSS)
∴∠BAM=∠BCM,
∴∠BCM=∠MCQ,且∠BCM+∠MCQ=180°,
∴∠BCM=∠MCQ=∠PAM=90°,且∠APM=45°,
∴∠APM=∠AMP=45°,
∴AP=AM,
∵∠PAO+∠MAO=90°,∠MAO+∠AMO=90°,
∴∠PAO=∠AMO,且∠PEA=∠AOM=90°,AM=AP,
∴△APE≌△MAO(AAS)
∴AE=OM,PE=AO=3,
∴2m﹣6=3,
∴m=![]() ,
,
∴Q(![]() ,﹣3),P(﹣
,﹣3),P(﹣![]() ,3),
,3),
设直线PQ的解析式为:y=ax+c,
∴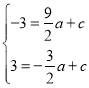 ,解得:
,解得: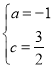 ,
,
∴直线PQ的解析式为:y=﹣x+![]() .
.


科目:初中数学 来源: 题型:
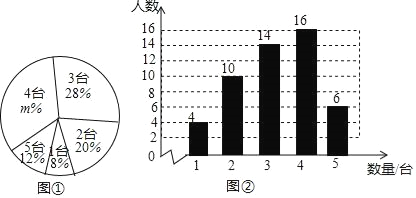
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
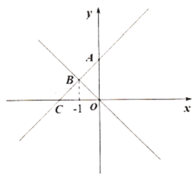
【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴和
轴和![]() 轴交于
轴交于![]() ,
,![]() 两点,且与正比例函数
两点,且与正比例函数![]() 的图象交于点
的图象交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求正比例函数的表达式;
(3)点![]() 是一次函数图象上的一点,且
是一次函数图象上的一点,且![]() 的面积是3,求点
的面积是3,求点![]() 的坐标;
的坐标;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的值最小?若存在,求出点
的值最小?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
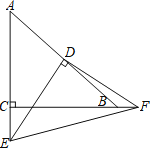
【题目】如图,已知Rt △ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB的延长线于E、F.下面结论一定成立的是______.(填序号)
①CD=![]() AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,AB=AC,∠BAC=90°
(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF
①求证:△AED≌△AFD;
②当BE=3,CE=7时,求DE的长;
(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
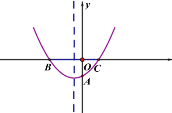
【题目】如图,二次函数y=ax2+bx+c 的图象与 x 轴交于 B、C 两点,交 y 轴于点 A.
(1)根据图象请用“>”、“<”或“=”填空:a 0,b 0,c 0;
(2)如果 OC=OA=![]() OB,BC=3,求这个二次函数的解析式;
OB,BC=3,求这个二次函数的解析式;
(3) 在(2)中抛物线的对称轴上,存在点 Q 使得△OQA 的周长最短,试求出点 Q 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两商店出售同样的茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,两家商店搞促销活动,甲店:买一只茶壶赠一只茶杯;乙店:按定价的9折优惠,某顾客需购买茶壶4只,茶杯若干只(不少于4只).
(1)设购买茶杯数为![]() (只),在甲店购买的付款为
(只),在甲店购买的付款为![]() (元),在乙店购买的付款数为
(元),在乙店购买的付款数为![]() (元),分别写出在两家商店购物的付款数与茶杯数
(元),分别写出在两家商店购物的付款数与茶杯数![]() 之间的关系式;
之间的关系式;
(2)当购买多少只茶杯时,两家商店的花费相同?
(3)当购买20只茶杯时,去哪家商店购物比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
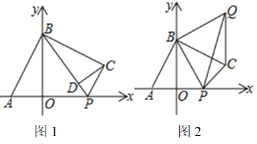
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com