
【题目】如图,已知Rt △ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB的延长线于E、F.下面结论一定成立的是______.(填序号)
①CD=![]() AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
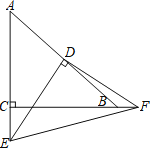
【答案】①②
【解析】
连接CD,如图,利用直角三角形斜边上的中线性质可对①进行判断;再证明△CDE≌△BDF可对②进行判断;利用△DEF为等腰直角三角形得到![]() 根据三角形面积公式得到
根据三角形面积公式得到![]() 则可对③进行判断;然后计算
则可对③进行判断;然后计算![]() 则可对④进行判断.
则可对④进行判断.
解:连接CD,如图,
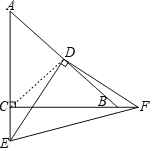
∵∠C=90°,D为AB边的中点,
∴CD=AD=DB,即![]() 所以①正确;
所以①正确;
∵CA=CB,∠C=90°,
∴∠ABC=45°,CD⊥BD,
∴∠DCE=135°,∠DBF=135°,
∵∠EDF=90°,
∴∠CDE=∠BDF,
在△CDE和△BDF中
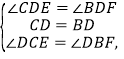
∴△CDE≌△BDF,
∴DE=DF,所以②正确;
∴△DEF为等腰直角三角形,
∴![]()
∴![]()
而EF2=CE2+CF2,
∴![]()
而![]()
∴
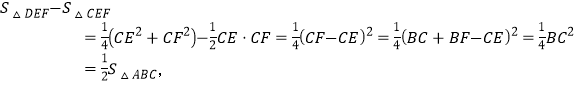
所以③④错误.
故答案为:①②.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合; ③若![]() 与
与![]() 成轴对称,则
成轴对称,则![]() 一定与
一定与![]() 全等;④有一个角是
全等;④有一个角是![]() 度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点P在△ABC内,PA=2,将PAB绕点A逆时针旋转得到△QAC,则PQ的长等于( )
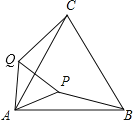
A. 2
B. ![]()
C. ![]()
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数y=﹣2x+1,下列结论正确的是( )
A.y值随x值的增大而增大
B.它的图象与x轴交点坐标为(0,1)
C.它的图象必经过点(﹣1,3)
D.它的图象经过第一、二、三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),△ABC和△AOD都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系与位置关系;
(2)如图(2),将图(1)中的△ABC绕点A顺时针施转α(0°<α<360°),那么(1)中线段BE与线段CD的关系是否还成立?如果成立,请你结合图(2)给出的情形进行证明;如果不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且AB=BC.
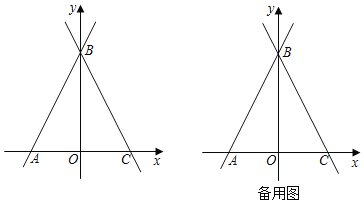
(1)求直线BC的解析式;
(2)点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);
(3)在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在⊙O上,∠BAD的平分线交⊙O于点C,过点C作CE⊥AD于点E,过点E作EH⊥AB于点H,交AC于点G,交⊙O于点F、M,连接BC.
(1)求证:EC是⊙O的切线;
(2)若AG=GC,试判断AG与GH的数量关系,并说明理由;
(3)在(2)的条件下,若⊙O的半径为4,求FM的长.
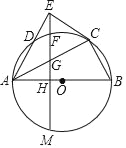
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com