
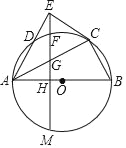
【题目】如图,AB是⊙O的直径,点D在⊙O上,∠BAD的平分线交⊙O于点C,过点C作CE⊥AD于点E,过点E作EH⊥AB于点H,交AC于点G,交⊙O于点F、M,连接BC.
(1)求证:EC是⊙O的切线;
(2)若AG=GC,试判断AG与GH的数量关系,并说明理由;
(3)在(2)的条件下,若⊙O的半径为4,求FM的长.
【答案】(1)见解析;(2)AG=2GH,理由见解析;(3)2![]() .
.
【解析】
(1)连接OC,求出OC∥AE,求出EC⊥OC,根据切线的判定得出即可;
(2)求出△EGC是等边三角形,求出∠EGC=60°,求出∠OAC=30°,即可得出答案;
(3)连接OF,根据垂径定理求出FM=2FH,根据勾股定理求出AH,求出OH,根据勾股定理求出FH,即可得出答案.
(1)证明:连接OC,
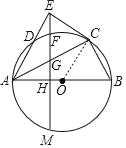
∵OA=OC,
∴∠ACO=∠OAC,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴OC∥AE,
∵CE⊥AE,
∴CE⊥OC,
∵OC过O,
∴EC是⊙O的切线;
(2)解:AG=2GH,
理由是:∵CE是⊙O切线,
∴∠OCE=90°,
∴∠OCA+∠ECA=90°,
∵EM⊥AB,
∴∠EHA=∠EHO=90°,
∴∠OAC+∠AGH=90°,
∵∠OAC=∠OCA,
∴∠AGH=∠ECA,
∵∠EGC=∠AGH,
∴∠EGC=∠ECG,
∴EC=EG,
∵∠AEC=90°,AG=GC=![]() AC,
AC,
∴EG=![]() AC,
AC,
∴EC=![]() AC,
AC,
∴EG=EC=CG,
∴△EGC是等边三角形,
∴∠EGC=60°,
∴∠AGH=∠EGC=60°,
∴∠OAC=30°,
∵∠GHA=90°,
∴AG=2GH;
(3)解:连接OF,
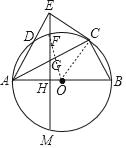
∵AB是直径,
∴∠ACB=90°,AB=2OA=2×4=8,
∵∠OAC=30°,
∴BC=![]() AB=4,
AB=4,
在Rt△ACB中,AC=![]() =
=![]() =4
=4![]() ,
,
∵AG=![]() AC,
AC,
∴AG=2![]() ,
,
∵AG=2GH,
∴GH=![]() ,
,
在Rt△AGH中,AH=![]() =
=![]() =3,
=3,
∴OH=OA﹣AH=4﹣3=1,
在Rt△FHO中,FH=![]() =
=![]() =
=![]() ,
,
由垂径定理得:PM=2FH=2![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
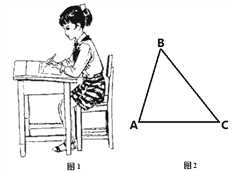
【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿,把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC,BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin530≈0.8,cos530≈0.6,tan530≈1.3)
查看答案和解析>>
科目:初中数学 来源: 题型:
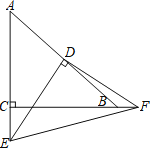
【题目】如图,已知Rt △ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB的延长线于E、F.下面结论一定成立的是______.(填序号)
①CD=![]() AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
AB;②DE=DF;③S△DEF=2S△CEF;④S△DEF-S△CEF=S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
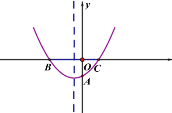
【题目】如图,二次函数y=ax2+bx+c 的图象与 x 轴交于 B、C 两点,交 y 轴于点 A.
(1)根据图象请用“>”、“<”或“=”填空:a 0,b 0,c 0;
(2)如果 OC=OA=![]() OB,BC=3,求这个二次函数的解析式;
OB,BC=3,求这个二次函数的解析式;
(3) 在(2)中抛物线的对称轴上,存在点 Q 使得△OQA 的周长最短,试求出点 Q 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两商店出售同样的茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,两家商店搞促销活动,甲店:买一只茶壶赠一只茶杯;乙店:按定价的9折优惠,某顾客需购买茶壶4只,茶杯若干只(不少于4只).
(1)设购买茶杯数为![]() (只),在甲店购买的付款为
(只),在甲店购买的付款为![]() (元),在乙店购买的付款数为
(元),在乙店购买的付款数为![]() (元),分别写出在两家商店购物的付款数与茶杯数
(元),分别写出在两家商店购物的付款数与茶杯数![]() 之间的关系式;
之间的关系式;
(2)当购买多少只茶杯时,两家商店的花费相同?
(3)当购买20只茶杯时,去哪家商店购物比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店购进一批秋衣,价格为每件30元.物价部门规定其销售单价不高于每件70元,经市场调查发现:日销售量y(件)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式.
(2)求该服装店要想销售这批秋衣日获利750元,售价应定多少元?
(3)请销售单价为多少元时,该服装店日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与射线
长为半径画弧,与射线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() ,垂足为
,垂足为![]() .
.

(1)线段![]() 与图中现有的哪一条线段相等?你得出的结论是:
与图中现有的哪一条线段相等?你得出的结论是:![]() ;
;
(2)证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com