
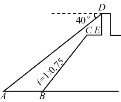
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为__米.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
【答案】5.1.
【解析】
延长DE交AB延长线于点P,作CQ⊥AP,可得CE=PQ=2、CQ=PE,由坡度i=1:0.75,可设CQ=4x、BQ=3x,根据BQ2+CQ2=BC2求得x的值,即可知DP=11,由AP的长以及AB=AP-BQ-PQ可得答案.
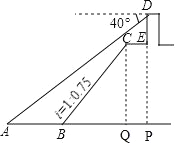
如图,延长DE交AB延长线于点P,作CQ⊥AP于点Q,
∵CE∥AP,
∴DP⊥AP,
∴四边形CEPQ为矩形,
∴CE=PQ=2,CQ=PE,
∵i= ![]() ,
,
∴设CQ=4x、BQ=3x,
由![]() 可得,
可得, ![]() ,
,
解得:x=2或x=2(舍去),
则CQ=PE=8,BQ=6,
∴DP=DE+PE=11,
在Rt△ADP中,∵![]() ,
,
∴AB=APBQPQ=13.162=5.1,
故答案为:5.1米


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】对于代数式ax2+bx+c(a≠0),下列说法正确的是( )
①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则a![]() +bx+c=a(x-p)(x-q)
+bx+c=a(x-p)(x-q)
②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c
③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
A. ③ B. ①③ C. ②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
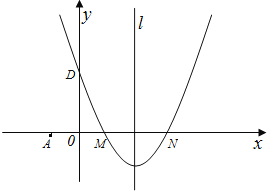
查看答案和解析>>
科目:初中数学 来源: 题型:
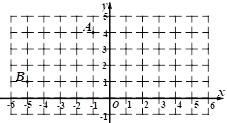
【题目】点A(1,4)和点B(5,1)在平面直角坐标系中的位置如图所示:
(1)点A1、B1分别为点A、B关于y轴的对称点,请画出四边形AA1B1B,并写出A1、B1的坐标;
(2)在(1)的条件下,画一条过四边形AA1B1B的一个顶点的线段,将四边形AA1B1B分成两个图形,并且使分得的图形中的一个是轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①②,锐角的正弦值和余弦值都随着锐角的变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在横线上填写“<”“>”或“=”):
若α=45°,则sin α cos α;
若α<45°,则sin α cos α;
若α>45°,则sin α cos α.
(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:sin 10°,cos 30°,sin 50°,cos 70°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.

(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
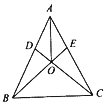
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com