
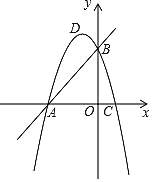
【题目】如图,直线y=x+3与两坐标轴交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)求A、B两点的坐标;
(2)求抛物线的解析式和点C的坐标.
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确( )?

A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
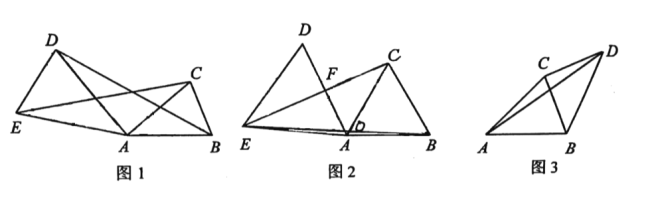
【题目】已知![]() 中,
中,![]() .
.
(1)如图1,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图3,在![]() 中,
中,![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
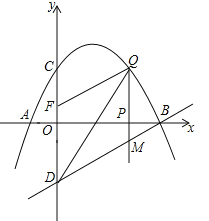
【题目】如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线![]() 交抛物线于点Q,交直线BD于点M.
交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com