
【题目】如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线![]() 交抛物线于点Q,交直线BD于点M.
交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
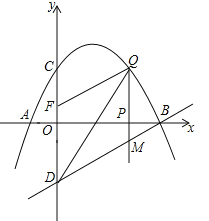
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形.
x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形.
【解析】
(1)待定系数法求解可得;
(2)先利用待定系数法求出直线BD解析式为y=![]() x﹣2,则Q(m,﹣
x﹣2,则Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
m﹣2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
(1)由抛物线过点A(﹣1,0)、B(4,0)可设解析式为y=a(x+1)(x﹣4),将点C(0,2)代入,得:﹣4a=2,解得:a=﹣![]() ,则抛物线解析式为y=﹣
,则抛物线解析式为y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)由题意知点D坐标为(0,﹣2),设直线BD解析式为y=kx+b,将B(4,0)、D(0,﹣2)代入,得:![]() ,解得:
,解得: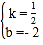 ,∴直线BD解析式为y=
,∴直线BD解析式为y=![]() x﹣2.
x﹣2.
∵QM⊥x轴,P(m,0),∴Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),则QM=﹣
m﹣2),则QM=﹣![]() m2+
m2+![]() m+2﹣(
m+2﹣(![]() m﹣2)=﹣
m﹣2)=﹣![]() m2+m+4.
m2+m+4.
∵F(0,![]() )、D(0,﹣2),∴DF=
)、D(0,﹣2),∴DF=![]() .
.
∵QM∥DF,∴当﹣![]() m2+m+4=
m2+m+4=![]() 时,四边形DMQF是平行四边形,解得:m=﹣1或m=3,即m=﹣1或m=3时,四边形DMQF是平行四边形.
时,四边形DMQF是平行四边形,解得:m=﹣1或m=3,即m=﹣1或m=3时,四边形DMQF是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=4,AD=3,AB⊥AD ,BC=12.
(1)求BD的长;
(2)当CD为何值时,△BDC是以CD为斜边的直角三角形?
(3)在(2)的条件下,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数![]() (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
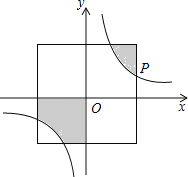
查看答案和解析>>
科目:初中数学 来源: 题型:
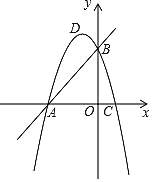
【题目】如图,直线y=x+3与两坐标轴交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)求A、B两点的坐标;
(2)求抛物线的解析式和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生参加数学素质测试(有四项),每项测试成绩采用百分制,成绩如表:
学生 | 数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | 平均成绩 | 方差 |
甲 | 87 | 93 | 91 | 85 | 89 | ______ |
乙 | 89 | 96 | 91 | 80 | ______ | ______ |
(1)将表格中空缺的数据补充完整,根据表中信息判断哪个学生数学综合素质测试成绩更稳定?请说明理由.
(2)若数与代数、空间与图形、统计与概率、综合与实践的成绩按![]() ,计算哪个学生数学综合素质测试成绩更好?请说明理由.
,计算哪个学生数学综合素质测试成绩更好?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交CD于点G,AD=AE.若AD=5,DE=6,则AG的长是( )

A. 6B. 8C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
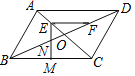
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AB=OB,点E、点F分别是OA、OD的中点,连接EF,∠CEF=45°,EM⊥BC于点M,EM交BD于点N,FN=![]() ,则线段BC的长为_____.
,则线段BC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答问题:
问题:分解因式:![]() .
.
解答:把![]() 带入多项式
带入多项式![]() ,发现此多项式的值为0,由此确定多项式
,发现此多项式的值为0,由此确定多项式![]() 中有因式
中有因式![]() ,于是可设
,于是可设![]() ,分别求出
,分别求出![]() ,
,![]() 的值.再代入
的值.再代入![]() ,就容易分解多项式
,就容易分解多项式![]() ,这种分解因式的方法叫做“试根法”.
,这种分解因式的方法叫做“试根法”.
(1)求上述式子中![]() ,
,![]() 的值;
的值;
(2)请你用“试根法”分解因式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
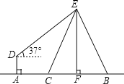
【题目】如图,在电线杆上的![]() 处引拉线
处引拉线![]() 和
和![]() 固定电线杆,在离电线杆
固定电线杆,在离电线杆![]() 米的
米的![]() 处安置测角仪(点
处安置测角仪(点![]() ,
,![]() ,
,![]() 在一直线上),在
在一直线上),在![]() 处测得电线杆上
处测得电线杆上![]() 处的仰角为
处的仰角为![]() ,已知测角仪的高
,已知测角仪的高![]() 为
为![]() 米,
米,![]() 为
为![]() 米,求拉线
米,求拉线![]() 的长.(精确到
的长.(精确到![]() 米)
米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com