
【题目】已知抛物线![]() 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
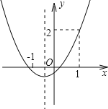
A. ①② B. ②③ C. ③④ D. ②④
【答案】D
【解析】
根据二次函数图像判断a,b,c的符号,根据图像上的(1,2)得到a+b+c的值,根据a-b+c<0和a+b+c=2求出b的范围,根据对称轴的范围和b的范围求a的范围.
①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为x=![]() <0,∴a、b同号,即b>0,
<0,∴a、b同号,即b>0,
∴abc<0,故本选项错误;
②当x=1时,函数值为2,
∴a+b+c=2;
故本选项正确;
④当x=-1时,函数值<0,
即a-b+c<0,(1)
又a+b+c=2,
将a+c=2-b代入(1),
2-2b<0,
∴b>1
③∵对称轴x=![]() >-1, 解得:
>-1, 解得:![]() <a,∵b>1,∴a>
<a,∵b>1,∴a>![]() ,故本选项错误;故本选项正确;
,故本选项错误;故本选项正确;
综上所述,其中正确的结论是②④;
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]() ;
;
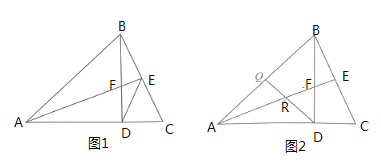
(2)如图1,连结![]() ,问
,问![]() 是否为
是否为![]() 的平分线?请说明理由.
的平分线?请说明理由.
(3)如图2,![]() 为
为![]() 的中点,连结
的中点,连结![]() 交
交![]() 于
于![]() ,用等式表示
,用等式表示![]() 与
与![]() 的数量关系?并给出证明.
的数量关系?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
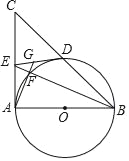
【题目】已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)G是ED上一点,连接BE交圆于F,连接AF并延长交ED于G.若GE=2,AF=3,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
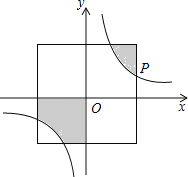
【题目】如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数![]() (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,﹣3),B(5,﹣1),C(1,3),结合所给的平面直角坐标系,解答下列问题:
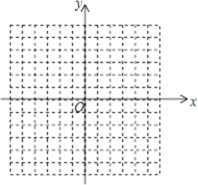
(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于y轴对称的△A'B'C',并写出△A'B'C'各顶点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
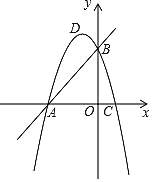
【题目】如图,直线y=x+3与两坐标轴交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)求A、B两点的坐标;
(2)求抛物线的解析式和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生参加数学素质测试(有四项),每项测试成绩采用百分制,成绩如表:
学生 | 数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | 平均成绩 | 方差 |
甲 | 87 | 93 | 91 | 85 | 89 | ______ |
乙 | 89 | 96 | 91 | 80 | ______ | ______ |
(1)将表格中空缺的数据补充完整,根据表中信息判断哪个学生数学综合素质测试成绩更稳定?请说明理由.
(2)若数与代数、空间与图形、统计与概率、综合与实践的成绩按![]() ,计算哪个学生数学综合素质测试成绩更好?请说明理由.
,计算哪个学生数学综合素质测试成绩更好?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AB=OB,点E、点F分别是OA、OD的中点,连接EF,∠CEF=45°,EM⊥BC于点M,EM交BD于点N,FN=![]() ,则线段BC的长为_____.
,则线段BC的长为_____.
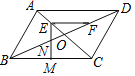
查看答案和解析>>
科目:初中数学 来源: 题型:
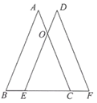
【题目】如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形;
(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com