
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]() ;
;
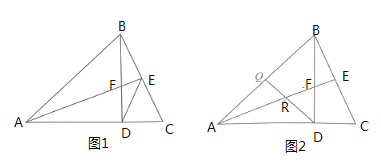
(2)如图1,连结![]() ,问
,问![]() 是否为
是否为![]() 的平分线?请说明理由.
的平分线?请说明理由.
(3)如图2,![]() 为
为![]() 的中点,连结
的中点,连结![]() 交
交![]() 于
于![]() ,用等式表示
,用等式表示![]() 与
与![]() 的数量关系?并给出证明.
的数量关系?并给出证明.
【答案】(1)证明见解析;(2)![]() 是
是![]() 的平分线,理由见解析;(3)
的平分线,理由见解析;(3)![]() ,证明过程见解析.
,证明过程见解析.
【解析】
(1)先根据等腰三角形的性质、三角形的内角和定理可求出![]() ,再根据三角形全等的判定定理与性质即可得证;
,再根据三角形全等的判定定理与性质即可得证;
(2)如图1(见解析),过点D分别作![]() ,由题(1)两个三角形全等可得
,由题(1)两个三角形全等可得![]() ,再根据三角形全等的判定定理与性质
,再根据三角形全等的判定定理与性质![]() ,最后根据角平分线的判定即可得出结论;
,最后根据角平分线的判定即可得出结论;
(3)如图2(见解析),连接BR,先根据等腰三角形的性质、垂直平分线的性质可得![]() ,从而可求得
,从而可求得![]() ,再根据勾股定理可得
,再根据勾股定理可得![]() ,最后根据等腰三角形的性质、等量代换即可得出答案.
,最后根据等腰三角形的性质、等量代换即可得出答案.
(1)![]()
![]()
![]() 是等腰直角三角形,且
是等腰直角三角形,且![]()
![]()
![]() (等腰三角形的三线合一性)
(等腰三角形的三线合一性)
在等腰![]() 中,
中,![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]() ;
;
(2)![]() 是
是![]() 的平分线,理由如下:
的平分线,理由如下:
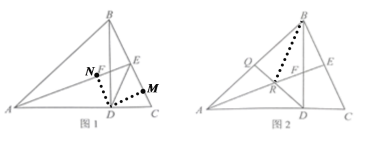
如图1,过点D分别作![]() ,则
,则![]()
由(1)已证:![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,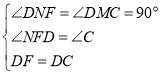
![]()
![]()
![]() 是
是![]() 的平分线;
的平分线;
(3)![]() ,证明过程如下:
,证明过程如下:
如图2,连接BR
由(1)已证:![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]() 为底边
为底边![]() 的中点
的中点
![]() (等腰三角形的三线合一性)
(等腰三角形的三线合一性)
![]() 是AB的垂直平分线
是AB的垂直平分线
![]()
![]()
![]()
![]()
![]()
![]()
则在![]() 中,
中,![]()
![]()
故![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】某校的大学生自愿者参与服务工作,计划组织全校自愿者统一乘车去某地.若单独调配![]() 座客车若干辆,则空出
座客车若干辆,则空出![]() 个座位,若只调配
个座位,若只调配![]() 座客车若干辆,则用车数量将增加
座客车若干辆,则用车数量将增加![]() 辆,并有
辆,并有![]() 人没有座位.
人没有座位.
(1)计划调配![]() 座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
(2)若同时调配![]() 座和
座和![]() 座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
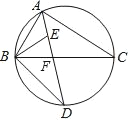
【题目】如图,∠BAC的平分线交AABC的外接圆于点D,交BC于点F,∠ABC的平分线交AD于点E.
(1)求证:DE=DB.
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径;
(3)若BD=6,DF=4,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
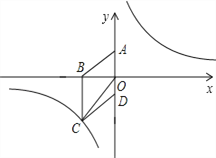
【题目】已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b-![]() <0的解集(直接写出答案).
<0的解集(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且![]() (0,3)、
(0,3)、![]() (﹣4,0).
(﹣4,0).
(1)求经过点![]() 的反比例函数的解析式;
的反比例函数的解析式;
(2)设![]() 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以![]() 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这五个数中,任取一个数作为
这五个数中,任取一个数作为![]() 的值,恰好使得关于
的值,恰好使得关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,且使两个根都在
有两个不相等的实数根,且使两个根都在![]() 和
和![]() 之间(包括
之间(包括![]() 和
和![]() ),则取到满足条件的
),则取到满足条件的![]() 值的概率为________.
值的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com