
【题目】寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?
【答案】(1)每副围棋16元,每副中国象棋10元;(2)最多可以购买25副围棋;
【解析】
(1)可设每副围棋![]() 元,每副中国象棋
元,每副中国象棋![]() 元,根据“若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元”可列出关于x,y的二元一次方程组,用消元法解之即可.(2)由(1)可知一副围棋和象棋的价格,可设购买围棋
元,根据“若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元”可列出关于x,y的二元一次方程组,用消元法解之即可.(2)由(1)可知一副围棋和象棋的价格,可设购买围棋![]() 副,“购买围棋和中国象棋共40副”,知购买象棋
副,“购买围棋和中国象棋共40副”,知购买象棋![]() 副,根据“总费用不超过550元”可列出关于z的一元一次不等式组,求出z的解集,取最大值即可.
副,根据“总费用不超过550元”可列出关于z的一元一次不等式组,求出z的解集,取最大值即可.
解:(1)设每副围棋![]() 元,每副中国象棋
元,每副中国象棋![]() 元,
元,
根据题意得:![]() ,
,
∴![]() ,
,
∴每副围棋16元,每副中国象棋10元;
(2)设购买围棋![]() 副,则购买象棋
副,则购买象棋![]() 副,
副,
根据题意得:![]() ,
,
∴![]() ,
,
∴最多可以购买25副围棋;


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为 ![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D.“抛一枚正方体骰子,朝上的点数为2的概率为 ![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 ![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2= ![]() (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
②k=4;
③当0<x<2时,y1<y2;
④如图,当x=4时,EF=4.
其中正确结论的个数是( )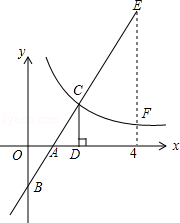
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
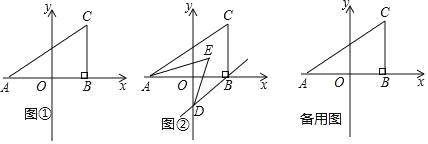
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解中学2 000名学生家长对“中学生骑电动车上学”的态度,从中随机调查400名家长,结果有360名家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查
B. 该校只有360名家长持反对态度
C. 样本是360名家长
D. 该校约有90%的家长持反对态度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com