
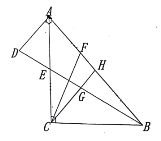
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.![]() 为
为![]() 中点,
中点,![]() 交
交![]() 于
于![]() ,
,![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,且
,且![]() .
.
(1)若![]() ,求
,求![]() 的长度;
的长度;
(2)求证:![]() .
.
【答案】(1)HG=2;(2)证明见解析.
【解析】
(1)利用ASA证明△AFC≌△CBG,从而可得CG=AF=3,根据直角三角形斜边上的中线等于斜边的一半可得CH=5,再根据HG=CH-CG即可得答案;
(2)由等腰三角形的性质可得CH⊥AB,继而证得CH∥AD,得到BG=DG,再根据AE=CE证明△ADE与△CGE全等,从而得到DE=FG,进而则可得到结论.
(1)∵∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,
又∵H为AB的中点,AB=10,
∴∠BCG=![]() ∠ACB=45°,CH=
∠ACB=45°,CH=![]() AB=
AB=![]() =5,
=5,
∴∠BCG=∠CAF,
又∵AC=CB,∠ACF=∠CBG,
∴△ACF≌△CBG(ASA),
∴CG=AF=3,
∴HG=CH-CG=5-3=2;
(2)∵AC=BC,H为AB的中点,
∴CH⊥AB,
又∵AD⊥AB,
∴AD//CH,
∴GH是△BAD的的中位线,
∴BG=DG,
∵AD//CH,
∴∠DAE=∠GCE,∠D=∠∠CGE,
又∵AE=CE,
∴△ADE≌△CGE(AAS),
∴DE=GE,
∴DG=DE+EG=2EG,
∵△ACF≌△CBG,
∴CF=BG,
∴CF=2EG.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() 平分
平分![]() ,且
,且![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() .
.
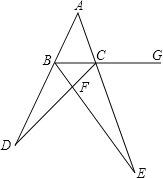
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数;
的度数;
![]() 若在图中继续作
若在图中继续作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,以此类推,作
,以此类推,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,请用含有
,请用含有![]() 的式了表示
的式了表示![]() 的度数(直接写答案).
的度数(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学“书香文化进校园”活动筹备小组准备购买![]() 两种类型的毛笔,已知购买一支
两种类型的毛笔,已知购买一支![]() 类型的毛笔比购买一支
类型的毛笔比购买一支![]() 类型的毛笔多花30元;且购买
类型的毛笔多花30元;且购买![]() 类型的毛笔80与购买
类型的毛笔80与购买![]() 类型的毛笔50支的价格相同.
类型的毛笔50支的价格相同.
(1)求![]() 两种类型毛笔的单价各是多少?
两种类型毛笔的单价各是多少?
(2)由于报名人数超过预期,筹备小组决定再次购买![]() 两种类型毛笔共50支.然而商店对商品价格进行了调整,
两种类型毛笔共50支.然而商店对商品价格进行了调整,![]() 类型毛笔售价比第一次购买时提高4元,B类型毛笔售价按第一次购买时售价的9折出售,如果此次购买
类型毛笔售价比第一次购买时提高4元,B类型毛笔售价按第一次购买时售价的9折出售,如果此次购买![]() 两种类型毛笔的总费用不超过3150元且保证这次购买的
两种类型毛笔的总费用不超过3150元且保证这次购买的![]() 种类型毛笔不少于23支,则这次购买方案有哪几种?
种类型毛笔不少于23支,则这次购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
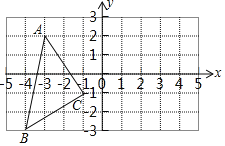
【题目】如图,在平面直角坐标系中,△ABC的顶点A、B、C坐标分别为(﹣3,2),(﹣4,﹣3),(﹣1,﹣1).
(1)画出△ABC关于y轴对称的△A1B1C1;(A、B、C的对称点分别为A1、B1、C1)
(2)写出△A1B1C1各顶点A1、B1、C1的坐标.A1 、B1 、C1
(3)直接写出△ABC的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,1),B(1,2),点P在x轴上运动,当点P到A、B两点距离之差的绝对值最大时,点P的坐标是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com