
����Ŀ��ij��˾����Ƹһ�����ž������Լס��ҡ���������ѡ�˽������������ʲ��ԣ�������Գɼ��������ʾ��
������Ŀ | ���Գɼ� | ||
�� | �� | �� | |
רҵ֪ʶ | 74 | 87 | 90 |
�������� | 58 | 74 | 70 |
�ۺ����� | 87 | 43 | 50 |
��1������ʵ����Ҫ����˾��רҵ֪ʶ�������������ۺ�����������Ե÷ְ�4��3��1�ı���ȷ��ÿ���˵IJ����ܳɼ�����ʱ˭����¼�ã�
��2�����������רҵ֪ʶ�������������ۺ�����������Ե÷ֵı�����ȷ��ÿ���˵IJ����ܳɼ���ʹ���ұ�¼�ã���������Ƶı���Ϊx��y��1����x+y+1��10����x���� ����y���� ������д��x��y��һ������ֵ���ɣ�
���𰸡���1����ʱ������¼�ã���2��1��8�����𰸲�Ψһ��
��������
��1���ȸ��ݼ�Ȩƽ�����ļ��㹫ʽ������˵��ܳɼ����ٱȽϴ�С���ɵã�
��2���ȷ����ҵ�����ɼ���ʹ��ɼ��ߵ���Ŀ��ռȨ�ؾ����ܴ��ٸ���![]() �ó�һ��x��y������ֵ��Ȼ�����ü�Ȩƽ�����ļ��㹫ʽ���м��鼴�ɣ�
�ó�һ��x��y������ֵ��Ȼ�����ü�Ȩƽ�����ļ��㹫ʽ���м��鼴�ɣ�
��1�����ܳɼ���![]() ���ҵ��ܳɼ���
���ҵ��ܳɼ���![]() �������ܳɼ���
�������ܳɼ���![]()
�ɴ˿�֪�������ܳɼ����
�ʴ�ʱ������¼�ã�
��2�����ҵ�רҵ����Ϊ87�֣�λ�ڵڶ�����������74�֣�λ�ڵ�һ�����ۺ�����43�֣�λ�ڵ���
��Ҫʹ���ұ�¼�ã�������������ռ��Ȩ��Ҫ�����ܴ�y�����ܴ�
��![]()
��ˣ�![]() ����
����
��������ã���![]() ʱ�����ܳɼ���
ʱ�����ܳɼ���![]() ���ҵ��ܳɼ���
���ҵ��ܳɼ���![]() �������ܳɼ���
�������ܳɼ���![]() ������Ҫ��
������Ҫ��
�ʴ�Ϊ��1��8�����𰸲�Ψһ��


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����εı߳�����![]() �������������У�
�������������У�![]() ���������㶼��С�����εĸ���ϣ���
���������㶼��С�����εĸ���ϣ���![]() �Ƶ�
�Ƶ�![]() ��ת
��ת![]() �õ�
�õ�![]() ����
����![]() ��
��![]() �ֱ����
�ֱ����![]() ��
��![]() ��Ӧ��������
��Ӧ��������![]() ��
��![]() ��
��
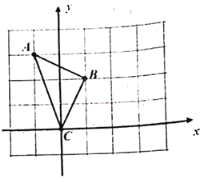
��1����ֱ���������в�ȫͼ�Σ�
��2���ı���![]() ���ܳ���________________�����ȵ�λ��
���ܳ���________________�����ȵ�λ��
��3��ֱ��д���ı���![]() �Ǻ���������ı��Σ�
�Ǻ���������ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ����
����![]() ��
��![]() �ڵĶ��㣬��
�ڵĶ��㣬��![]() ������
������![]() ��
��![]() �ֱ�������
�ֱ�������![]() ��
��![]() �����ڵ�
�����ڵ�![]() �Ķ��㣬��
�Ķ��㣬��![]() �ܳ�����Сֵ��______��
�ܳ�����Сֵ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ڼ䣬ij��λ8���쵼��320��Ա�������������������չ���������45����30��С����������2����3��С���������1700Ԫ��������3����2��С���������1800Ԫ
��1�����С��ÿ������Ѹ��Ƕ���Ԫ��
��2����ÿ����������Ҫ��һ���쵼��ÿ���˾�����λ����������ò�����3100Ԫ������ʡǮ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
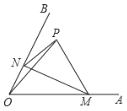
����Ŀ���ڵ���![]() �У�
�У�![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��![]() ����Ϊ
����Ϊ![]() ����֪
����֪![]() ��
��
��1����ͼ�٣���ֱ��![]() ����һ��
����һ��![]() ������
������![]() ����
����![]() ����֤��
����֤��![]() ��
��
��2����ͼ�ڣ���![]() ��
��![]() ����ƽ�ƣ��ֱ�
����ƽ�ƣ��ֱ�![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ʱ����
ʱ����![]() �������
�������
��3����ͼ�ۣ���ֱ��![]() ��
��![]() �������
�������![]() ����ƽ�Ƶ��ٶ�Ϊÿ��1����λ����
����ƽ�Ƶ��ٶ�Ϊÿ��1����λ����![]() ���ڵ�
���ڵ�![]() ��ͬʱ��һ����
��ͬʱ��һ����![]() ��
��![]() ���������ͬ���ٶ���
���������ͬ���ٶ���![]() ���˶�����
���˶�����![]() ��
��![]() ��
��![]() ��
��![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() ����
����![]() �����
�����![]() ʱ�����˶�ֹͣ�����Ƿ������
ʱ�����˶�ֹͣ�����Ƿ������![]() ��
��![]() ��
��![]() Ϊ������������ǵ��������Σ������ڣ�ֱ��д��
Ϊ������������ǵ��������Σ������ڣ�ֱ��д��![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���P��CD���е㣬��BCD=60��������AP��BC���ӳ����ڵ�E������BP��DE�ڵ�K����O���߶�BK���е㣮
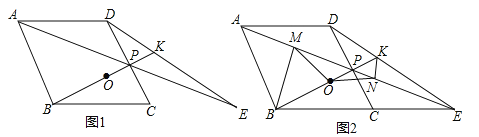
��1����֤����ADP�ա�ECP��
��2����BP=nPK�������n��ֵ��
��3����BM�AAE�ڵ�M����KN�AAE�ڵ�N������MO��NO����ͼ2��ʾ����֤����MON�ǵ��������Σ���ֱ��д����MON�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAC��30�㣬�� D Ϊ��BAC��һ�㣬�� E��F �ֱ���AB��AC�ϵĶ��㣮��AD��9�����DEF�ܳ�����СֵΪ____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ�ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ���������ֳ��Ŀ�С�����Σ�Ȼ��ͼ2����״ƴ��һ��������.


![]() ͼ2����Ӱ���ֵ������εı߳���______.
ͼ2����Ӱ���ֵ������εı߳���______.
![]() �����ֲ�ͬ�ķ�����ͼ����Ӱ���ֵ����.
�����ֲ�ͬ�ķ�����ͼ����Ӱ���ֵ����.
������1��![]() = ____________��
= ____________��
������2��![]() = ____________��
= ____________��
(3) �۲�ͼ2��д��(a+b)2,(a-b)2,ab����������ʽ֮��ĵ�����ϵ��
![]() ����
����![]() ���еĵ�����ϵ��������⣺��m+n=10,m-n=6����mn��ֵ.
���еĵ�����ϵ��������⣺��m+n=10,m-n=6����mn��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У� ADƽ�֡�CAB��BC�ڵ�E. ����BDA=90�㣬E��AD�е㣬DE=2��AB=5����AC�ij�Ϊ�� ��
�У� ADƽ�֡�CAB��BC�ڵ�E. ����BDA=90�㣬E��AD�е㣬DE=2��AB=5����AC�ij�Ϊ�� ��
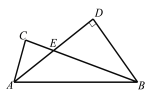
A.1B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com