
【题目】如图,∠BAC=30°,点 D 为∠BAC内一点,点 E,F 分别是AB,AC上的动点.若AD=9,则△DEF周长的最小值为____.

【答案】9;
【解析】
由对称的性质可得:DE=EM,DF=FN,AM=AD=AN=9,∠MAE=∠DAE,∠NAF=∠DAF,然后根据两点之间线段最短可得此时MN即为△DEF的周长的最小值,然后根据等边三角形的判定定理及定义即可求出结论.
解:过点D分别作AB、AC的对称点M、N,连接MN分别交AB、AC于点E、F,连接DE、DF、AD、AM和AN
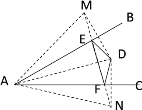
由对称的性质可得:DE=EM,DF=FN,AM=AD=AN=9,∠MAE=∠DAE,∠NAF=∠DAF
∴△DEF的周长=DE+EF+DF= EM+EF+FN=MN,∠MAE+∠NAF=∠DAE+∠DAF=∠BAC=30°
∴根据两点之间线段最短,此时MN即为△DEF的周长的最小值,∠MAN=∠MAE+∠NAF+∠BAC=60°
∴△MAN为等边三角形
∴MN=AM=AN=9
即△DEF周长的最小值为9
故答案为:9.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2016的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,∠B=30°,BC边上有一点P(不与点B,C重合),I为△APC的内心,若∠AIC的取值范围为m°<∠AIC<n°,则m+n=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
专业知识 | 74 | 87 | 90 |
语言能力 | 58 | 74 | 70 |
综合素质 | 87 | 43 | 50 |
(1)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(2)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PEEQ的值是( )
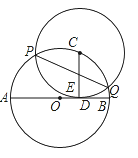
A. 24 B. 9 C. 36 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
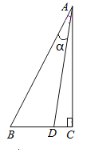
【题目】如图,已知Rt△ABC中,∠C=90°,∠BAC=30°,点D为边BC上的点,连接AD,∠BAD=α,点D关于AB的对称点为E,点E关于AC的对称点为G,线段EG交AB于点F,连接AE,DE,DG,AG.
(1)依题意补全图形;
(2)求∠AGE的度数(用含α的式子表示);
(3)猜想:线段EG与EF,AF之间是否存在一个数量关系?若存在,请写出这个数量关系并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com