
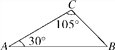
【题目】如图,已知AC=4,求AB和BC的长.
【答案】AB=2+2![]() ; BC=2
; BC=2![]()
【解析】试题分析:
根据三角形内角和不难求得∠B=45°. 由于∠A和∠B的角度值均为特殊角度值,所以可以利用AB边上的高(设该高为CD)将△ABC分成两个含有特殊角的直角三角形进行求解. 利用已知条件可以求解Rt△ADC,从而求得线段AD与CD的长. 由于线段CD为这两个直角三角形的公共边,并且已经求得∠B的值,所以Rt△CDB也是可解的. 解这个直角三角形,可以求得线段BC与BD的长,进而容易求得线段AB的长.
试题解析:

如图,过点C作CD⊥AB,垂足为D.
∵∠A=30°,AC=4,
∴在Rt△ADC中,
![]() ,
,
![]() ,
,
∵∠ACB=105°,∠A=30°,
∴在△ABC中,∠B=180°-∠A-∠ACB=180°-30°-105°=45°,
∵CD=2,
∴在Rt△CDB中,
![]() ,
,
![]() ,
,
∴AB=AD+BD=![]() .
.
综上所述,AB=![]() ,BC=
,BC=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】年初,工信部官网发布了2016年通信运营业统计公报,数据显示,2016年,4G用户数呈爆发式增长,全年新增3.4亿户,总数达到770 000 000亿户,将770 000 000用科学记数法表示应为( )
A.0.77×109
B.7.7×107
C.7.7×108
D.7.7×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?
②是否存在满足条件的点P,使得PC=![]() ?(不需说明理由).
?(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
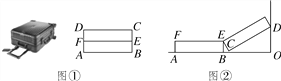
【题目】如图①所示的旅行箱的箱盖和箱底两部分的厚度相同,四边形ABCD为形如矩形的旅行箱一侧的示意图,F为AD的中点,EF∥CD.现将放置在地面上的箱子打开,使箱盖的一端点D靠在墙上,O为墙角,图②为箱子打开后的示意图.箱子厚度AD=30cm,宽度AB=50cm.
(1)图②中,EC=________cm,当点D与点O重合时,AO的长为________cm;
(2)若∠CDO=60°,求AO的长(结果取整数值,参考数据:sin60°≈0.87,cos60°=0.5,tan60°≈1.73,可使用科学计算器).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2015~2017)》,某市政府决定2015年投入6000万元用于改善医疗卫生服务,比2014年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2015年投入“需方”的资金将比2014年提高30%,投入“供方”的资金将比2014年提高20%.
(1)该市政府2014年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2015年投入“需方”和“供方”的资金是多少万元?
(3)该市政府预计2017年将有7260万元投入改善医疗卫生服务,若从2015~2017年每年的资金投入按相同的增长率递增,求2015~2017年的年增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com