
【题目】在等腰![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() 且
且![]() .
.![]() 是
是![]() 上一点,过
上一点,过![]() 作
作![]() 垂足为
垂足为![]() ,过
,过![]() 作
作![]() 垂足为
垂足为![]() ,已知
,已知![]() .
.
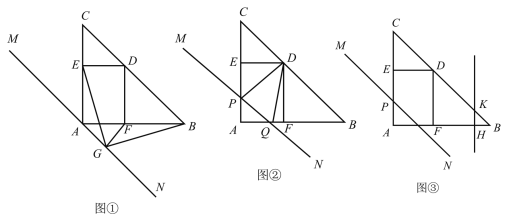
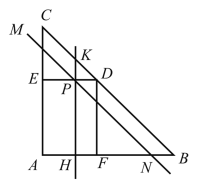
(1)如图①,在直线![]() 上有一点
上有一点![]() ,连接
,连接![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
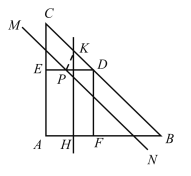
(2)如图②,将![]() 沿
沿![]() 方向平移,分别交
方向平移,分别交![]() 于
于![]() ,
,![]() 两点,当
两点,当![]() 时,求
时,求![]() 的面积;
的面积;
(3)如图③,设直线![]() 从
从![]() 点出发沿
点出发沿![]() 方向平移的速度为每秒1个单位,与
方向平移的速度为每秒1个单位,与![]() 交于点
交于点![]() ,同时有一动点
,同时有一动点![]() 从
从![]() 点出发以相同的速度向
点出发以相同的速度向![]() 点运动,过
点运动,过![]() 作
作![]() 交
交![]() 于
于![]() ,设运动时间为
,设运动时间为![]() ,当
,当![]() 到达点
到达点![]() 时所有运动停止,问是否存在以
时所有运动停止,问是否存在以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?若存在,直接写出
为顶点的三角形是等腰三角形?若存在,直接写出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)见解析;(2)5;(3)存在,t的值为1或5或![]() 或
或![]() .
.
【解析】
(1)根据条件证明△AGE≌△FGB,从而可得结论;
(2)根据![]() 得出AP和AQ,再根据
得出AP和AQ,再根据![]() 可求出AB和AC的长,从而求出△CDP和△BDQ的面积,即可求出△DPQ的面积;
可求出AB和AC的长,从而求出△CDP和△BDQ的面积,即可求出△DPQ的面积;
(3)分两段进行讨论:当点P在线段AE上时,DP=DK,当点P在线段ED上时,再分三种情况:DP=DK,PK=PD,KD=KP,分别找出等量关系,表示出线段长度,求解即可.
解:(1)∵∠BAC=90°,AB=AC,
∴∠C=∠B=45°,
∵MN∥BC,
∴∠BAG=∠B=45°,
∵∠AGF=∠BGE=90°,
∴∠AFG=45°,∠EAG=∠BFG,∠AGE=∠FGB,AG=FG,
在△AGE和△FGB中,
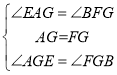 ,
,
∴△AGE≌△FGB(ASA),
∴BG=GE;
(2)∵MN∥BC,
∴∠MQA=∠NPA=45°,即△APQ为等腰直角三角形,
∵![]() ,
,
∴AP=AQ=2,
∵DE⊥AC,DF⊥AB,
∴△CED和△DFB是等腰直角三角形,
即CE=DE=AF=3,DF=BF=AE=4,
∴EP=2,QF=1,
∴S△DPQ=S△ABC-S△DPC-S△DBQ-S△APQ
=![]() ×AC×AB-
×AC×AB-![]() ×PC×DE-
×PC×DE-![]() ×BQ×DF-2
×BQ×DF-2
=![]() ×7×7-
×7×7-![]() ×5×3-
×5×3-![]() ×5×4-2
×5×4-2
=5,
∴△DPQ的面积为5;
(3)当点P在线段AE上时,∠PDK为钝角,
若△PDK为等腰三角形,则DP=DK,
此时,PE=4-t,AP= HB=HK =t,
∴DK=BD-BK=![]() -
-![]() BH=
BH=![]() ,DP=
,DP=![]() ,
,
∴DP2= DK2,
即![]()
解得:t=1或7(舍);
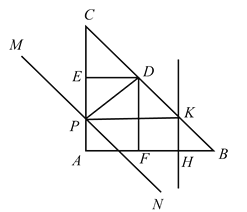
当点P在线段ED上时,K在线段CD上,
若KD=KP,此时∠CDE=45°,则△KDP为等腰直角三角形,
此时有EP+2HF=3,
∵EP=t-4,HF=t-4,
∴t-4+2(t-4)=3,
解得:t=5;
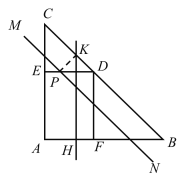
若PK=PD,此时∠CDE=45°,则△KDP为等腰直角三角形,
此时有:HF+EP=3,
∵HF=t-4,EP=t-4,
∴t-4+t-4=3,
解得:t=![]() ;
;
若DK=DP,
∵BK=![]() t,
t,
∴DK=![]() t -
t -![]() ,DP=7-t,
,DP=7-t,
∴![]() t -
t -![]() =7-t,
=7-t,
解得:t=![]() ;
;
综上:存在△DPK为等腰三角形,t的值为1或5或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
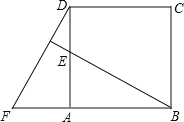
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=5,AB=9,求:
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,∠B=30°,BC边上有一点P(不与点B,C重合),I为△APC的内心,若∠AIC的取值范围为m°<∠AIC<n°,则m+n=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
专业知识 | 74 | 87 | 90 |
语言能力 | 58 | 74 | 70 |
综合素质 | 87 | 43 | 50 |
(1)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(2)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PEEQ的值是( )
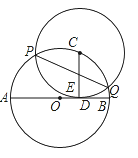
A. 24 B. 9 C. 36 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com